
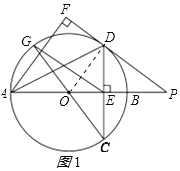
【题目】如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG.
(1)求证:DF是⊙O的切线;
(2)若AD=DP,OB=3,求![]() 的长度;
的长度;
(3)若DE=4,AE=8,求线段EG的长.

【答案】(1)证明见解析(2)π(3)2![]()
【解析】试题分析:(1)连接OD,由等腰三角形的性质得出∠DAB=∠ADO,再由已知条件得出∠ADO=∠DAF,证出OD∥AF,由已知DF⊥AF,得出DF⊥OD,即可得出结论;
(2)易得∠BOD=60°,再由弧长公式求解即可;
(3)连接DG,由垂径定理得出DE=CE=4,得出CD=8,由勾股定理求出DG,再由勾股定理求出EG即可.
试题解析:(1)证明:连接OD,如图1所示:
∵OA=OD,
∴∠DAB=∠ADO,
∵∠DAF=∠DAB,
∴∠ADO=∠DAF,
∴OD∥AF,
又∵DF⊥AF,
∴DF⊥OD,
∴DF是⊙O的切线;
(2)∵AD=DP
∴∠P=∠DAF=∠DAB =x0
∴∠P+∠DAF+∠DAB =3xo=90O
∴x0=300
∴∠BOD=60°,
∴![]() 的长度=
的长度=![]()
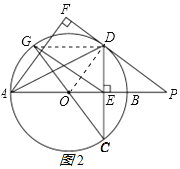
(3)解:连接DG,如图2所示:
∵AB⊥CD,
∴DE=CE=4,
∴CD=DE+CE=8,
设OD=OA=x,则OE=8﹣x,
在Rt△ODE中,由勾股定理得:OE2+DE2=OD2,
即(8﹣x)2+42=x2,
解得:x=5,
∴CG=2OA=10,
∵CG是⊙O的直径,
∴∠CDG=90°,
∴DG=![]() =6,
=6,
∴EG=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.

(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)等于371元,请通过计算求出该商场购进甲、乙两种牛奶各自多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
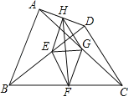
【题目】如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.结论:①EG⊥FH;②四边形EFGH是矩形;③HF平分∠EHG;④EG![]() BC;⑤四边形EFGH的周长等于2AB.其中正确的个数是( )
BC;⑤四边形EFGH的周长等于2AB.其中正确的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川广安8分)某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
空调 | 彩电 | |
进价(元/台) | 5400 | 3500 |
售价(元/台) | 6100 | 3900 |
设商场计划购进空调x台,空调和彩电全部销售后商场获得的利润为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择?
(3)选择哪种进货方案,商场获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
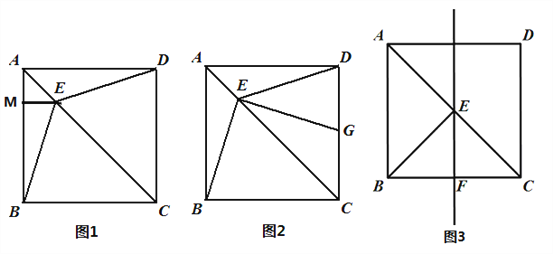
【题目】如图,在正方形ABCD中,AB=4,点E在对角线AC上,连接BE、DE,
(1)如图1,作EM⊥AB交AB于点M,当AE=![]() 时,求BE的长;
时,求BE的长;
(2)如图2,作EG⊥BE交CD于点G,求证:BE=EG;
(3)如图3,作EF⊥BC交BC于点F,设BF=x,△BEF的面积为y.当x取何值时,y取得最大值,最大值是多少?当△BEF的面积取得最大值时,在直线EF取点P,连接BP、PC,使得∠BPC=45°,求EP的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,AC=8cm,BC=6cm,D、E分别为边AB、BC的中点,连结DE,点P从点A出发,沿折线AD﹣DE运动,到点E停止,点P在AD上以5cm/s的速度运动,在DE上以1cm/s的速度运动,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN.设点P的运动时间为t(s).
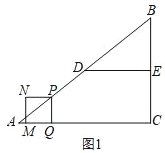
(1)当点P在线段DE上运动时,线段DP的长为_____cm.(用含t的代数式表示)
(2)当正方形PQMN与△ABC重叠部分图形为五边形时,设五边形的面积为S(cm2),求S与t的函数关系式,并写出t的取值范围.
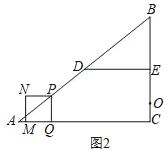
(3)如图2,若点O在线段BC上,且CO=1,以点O为圆心,1cm长为半径作圆,当点P开始运动时,⊙O的半径以0.2cm/s的速度开始不断增大,当⊙O与正方形PQMN的边所在直线相切时,求此时的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十·一”黄金周期间,武汉动物园在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)若9月30日的游客人数记为![]() ,请用
,请用![]() 的代数式表示10月2日的游客人数?
的代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由。
(3)若9月30日的游客人数为2万人,门票每人10元。问黄金周期间武汉动物园门票收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上有![]() 三个点,它们表示的数分别是
三个点,它们表示的数分别是![]() .
.
![]()
(1)填空:![]() ,
,![]() .
.
(2)若点![]() 以每秒
以每秒![]() 个单位长度的速度向左运动,同时,点
个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒
分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动.试探索:
个单位长度的速度向右运动.试探索:![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变? 请说明理由。
的变化而改变? 请说明理由。
(3)现有动点![]() 都从
都从![]() 点出发,点
点出发,点![]() 以每秒
以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 移动:当点
移动:当点![]() 移动到
移动到![]() 点时,点
点时,点![]() 才从
才从![]() 点出发,并以每秒
点出发,并以每秒![]() 个单位长度的速度向右移动,且当点
个单位长度的速度向右移动,且当点![]() 到达
到达![]() 点时,点
点时,点![]() 就停止移动.设点
就停止移动.设点![]() 移动的时间为
移动的时间为![]() 秒,请试用含
秒,请试用含![]() 的式了表示
的式了表示![]() 两点间的距离(不必写过程,直接写出结果).
两点间的距离(不必写过程,直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com