
分析 (1)根据x轴上点的坐标特征,计算函数值为0时所对应的自变量的值即可得到与x轴的交点A,B的坐标;
(2)根据两条直线相交的问题,解由两个解析式组成的方程组即可得到两函数的交点坐标;
(3)根据三角形面积公式求得即可.
解答 解:(1)当y=0时,-$\frac{1}{2}$x+1=0,解得x=2;2x+3=0,解得x=-$\frac{3}{2}$;
所以两直线与x轴交点A(2,0),B(-$\frac{3}{2}$,0);
(2)解$\left\{\begin{array}{l}{y=-\frac{1}{2}x+1}\\{y=2x+3}\end{array}\right.$得$\left\{\begin{array}{l}{x=-\frac{4}{5}}\\{y=\frac{7}{5}}\end{array}\right.$.
所以两直线交点C的坐标是(-$\frac{4}{5}$,$\frac{7}{5}$).
(3)S△ABC=$\frac{1}{2}$×(2+$\frac{3}{2}$)×$\frac{7}{5}$=$\frac{7}{20}$.
点评 本题考查了两条直线相交或平行的问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 36cm2 | B. | 12acm2 | C. | (36+12a)cm2 | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
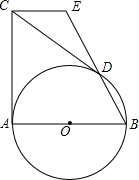 已知AB是圆O的直径,CA与圆O相切于A,且CA=AB=2,过C作圆O的切线CD,切点为D,连接BD并延长交过C与AB平行的直线于E,给出下列结论:①CE=1;②DE:BD=3:2;③S△CDE=$\frac{3}{5}$;④sin∠ECD=$\frac{2}{5}$.其中正确的结论是(只填序号)①②③.
已知AB是圆O的直径,CA与圆O相切于A,且CA=AB=2,过C作圆O的切线CD,切点为D,连接BD并延长交过C与AB平行的直线于E,给出下列结论:①CE=1;②DE:BD=3:2;③S△CDE=$\frac{3}{5}$;④sin∠ECD=$\frac{2}{5}$.其中正确的结论是(只填序号)①②③.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
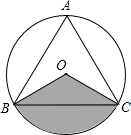 如图,等边△ABC内接于⊙O,AB=4$\sqrt{3}$.
如图,等边△ABC内接于⊙O,AB=4$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com