
【题目】已知二次函数 ![]() 的
的 ![]() 与
与 ![]() 的部分对应值如下表:
的部分对应值如下表:
| … | -1 | 0 | 1 | 3 | … |
| … | -3 | 1 | 3 | 1 | … |
则下列判断中正确的是( )
A.拋物线开口向上
B.拋物线与 ![]() 轴交于负半轴
轴交于负半轴
C.当 ![]() 时,
时, ![]()
D.方程 ![]() 的正根在3与4之间
的正根在3与4之间
【答案】D
【解析】由表可知,当 ![]() 和
和 ![]() 时,
时, ![]() .
.
由抛物线关于对称轴对称,可得出此函数的对称轴是 ![]()
根据表中y值的变化规律可知,在对称轴的左侧,y随x的增大而增大,在对称轴的右侧,y随x的增大而减小,
∴此抛物线开口向下,
故答案为:项A错误;
当 ![]() 时,根据表中数据可知
时,根据表中数据可知 ![]()
∴此抛物线与y轴交于点(0,1)
即拋物线与 ![]() 轴交于正半轴
轴交于正半轴
故答案为:项B错误;
由抛物线的对称性可知:当 ![]() 和
和 ![]() 时的函数值相等,即
时的函数值相等,即 ![]() ,
,
∴当 ![]() 时,
时, ![]() ,
,
故答案为:项C错误;
由表可知,当 ![]() 时,
时, ![]() ,
,
即抛物线与x轴的一个交点在-1和0之间,由抛物线的对称性可知,另一个交点应在3和4之间,
∴方程 ![]() 的正根在3与4之间.
的正根在3与4之间.
故答案为:D.
由表可知,当 y = 0 时, 1 < x < 0,即抛物线与x轴的一个交点在-1和0之间,由抛物线的对称性可知,另一个交点应在3和4之间,即方程 a a![]() + b x + c = 0 的正根在3与4之间.
+ b x + c = 0 的正根在3与4之间.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题:
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简)
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的![]() 满足
满足![]() ,求:①
,求:①![]() 的值;②
的值;②![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )

A. 8![]() B. 8 C. 4
B. 8 C. 4![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54,则∠B=( )

A. 54 B. 60 C. 72 D. 66
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寒假结束了,开学后小明对本校七年级部分同学寒假阅读总时间(结果保留整10小时)进行了抽样调查,所得数据整理后制作成如图所示的频数分布直方图.观察这个频数分布直方图,给出如下结论,正确的是( )
A.小明调查了100名同学
B.所得数据的众数是40小时
C.所得数据的中位数是30小时
D.全区有七年级学生6000名,寒假阅读总时间在20小时(含20小时)以上的约有5000名
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线![]() ,点E,F分别在直线AB,CD上,点M为两平行线内部一点.
,点E,F分别在直线AB,CD上,点M为两平行线内部一点.
(1)如图1,∠AEM,∠M,∠CFM的数量关系为________;(直接写出答案)
(2)如图2,∠MEB和∠MFD的角平分线交于点N,若∠EMF等于130°,求∠ENF的度数;
(3)如图3,点G为直线CD上一点,延长GM交直线AB于点Q,点P为MG上一点,射线PF、EH相交于点H,满足![]() ,
,![]() ,设∠EMF=α,求∠H的度数(用含α的代数式表示).
,设∠EMF=α,求∠H的度数(用含α的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
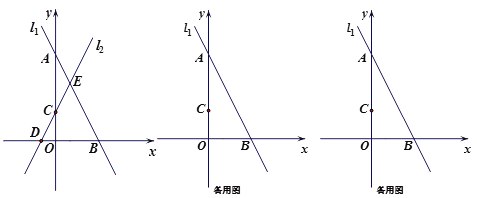
【题目】在平面直角坐标系中,直线l1:![]() 与坐标轴交于A,B两点,直线l2:
与坐标轴交于A,B两点,直线l2:![]() (
(![]() ≠0)与坐标轴交于点C,D.
≠0)与坐标轴交于点C,D.
(1)求点A,B的坐标;
(2)如图,当![]() =2时,直线l1,l2与相交于点E,求两条直线与
=2时,直线l1,l2与相交于点E,求两条直线与![]() 轴围成的△BDE的面积;
轴围成的△BDE的面积;
(3)若直线l1,l2与![]() 轴不能围成三角形,点P(a,b)在直线l2:
轴不能围成三角形,点P(a,b)在直线l2:![]() (k≠0)上,且点P在第一象限.
(k≠0)上,且点P在第一象限.
①求![]() 的值;
的值;
②若![]() ,,求
,,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com