
����Ŀ����֪��ֱ��![]() ����E��F�ֱ���ֱ��AB��CD�ϣ���MΪ��ƽ�����ڲ�һ�㣮
����E��F�ֱ���ֱ��AB��CD�ϣ���MΪ��ƽ�����ڲ�һ�㣮
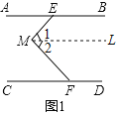
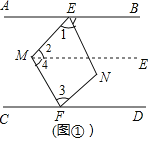
��1����ͼ1����AEM����M����CFM��������ϵΪ________��(ֱ��д����)
��2����ͼ2����MEB����MFD�Ľ�ƽ���߽��ڵ�N������EMF����130��������ENF�Ķ�����
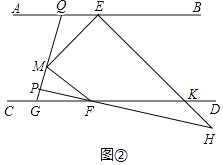
��3����ͼ3����GΪֱ��CD��һ�㣬�ӳ�GM��ֱ��AB�ڵ�Q����PΪMG��һ�㣬����PF��EH�ཻ�ڵ�H������![]() ��
��![]() ������EMF=��������H�Ķ���(�ú����Ĵ���ʽ��ʾ)��
������EMF=��������H�Ķ���(�ú����Ĵ���ʽ��ʾ)��

���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ��
��
��������
��1������![]() ��
��![]() ������ƽ���ߵ����ʿɵ�
������ƽ���ߵ����ʿɵ�![]() ��
��![]() ����
����![]() ���������������ɵý��ۣ�
���������������ɵý��ۣ�
��2����![]() ��
��![]() ������ƽ���ߵ������Լ���ƽ���ߵĶ�����㼴�ɣ�
������ƽ���ߵ������Լ���ƽ���ߵĶ�����㼴�ɣ�
��3����ͼ������![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ��֤��
��֤��![]() �����
�����![]() ���ɽ�����⣮
���ɽ�����⣮
��1����ͼ1������![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
��2����![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() �ֱ�ƽ��
�ֱ�ƽ��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
��3����ͼ������![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�����ڶ�Ԫһ�η��̵ĸ����У�������
��xy+2x��y��7����4x+1��x��y����![]() +y��5����x��y����x2��y2��2����6x��2y����x+y+z��1����y��y��1����2x2��y2+xy
+y��5����x��y����x2��y2��2����6x��2y����x+y+z��1����y��y��1����2x2��y2+xy
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ��� ![]() ��
�� ![]() ��
�� ![]() �IJ��ֶ�Ӧֵ���±���
�IJ��ֶ�Ӧֵ���±���
| �� | -1 | 0 | 1 | 3 | �� |
| �� | -3 | 1 | 3 | 1 | �� |
�������ж�����ȷ���ǣ� ��
A.�����߿�������
B.�������� ![]() �ύ�ڸ�����
�ύ�ڸ�����
C.�� ![]() ʱ��
ʱ�� ![]()
D.���� ![]() ��������3��4֮��
��������3��4֮��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O�İ뾶Ϊ ![]() ����AB=2����ABΪ�ױߣ���Բ�ڻ���0���ڽӵ�����ABC����ױ�AB���ϵĸ�CD��Ϊ�� ��
����AB=2����ABΪ�ױߣ���Բ�ڻ���0���ڽӵ�����ABC����ױ�AB���ϵĸ�CD��Ϊ�� ��
A.![]() +1
+1
B.![]() ��1
��1
C.![]() ��
�� ![]() ��1
��1
D.![]() +1��
+1�� ![]() +1
+1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ���飩�����ε����ߵ����ʣ������ε����ߵȷ������ε������
�����鷢չ������Ⱥ��߶αȵ���ϵ��
��1����ͼ1��MΪ��ABC��AB��һ�㣬��BM=2AM������ABC�����Ϊa������CBM�����ΪS����S=_______(�ú�a�Ĵ���ʽ��ʾ)��
������Ӧ�ã���2����ͼ2����֪��CDE�����Ϊ1��![]() ��
��![]() ������ABC�������
������ABC�������
��Ǩ��Ӧ�ã���3����ͼ3������ABC�У�M��AB�����ȷֵ�(![]() )��N��BC���е㣬����ABC�������1����ֱ��д���ı���BMDN�����Ϊ________��
)��N��BC���е㣬����ABC�������1����ֱ��д���ı���BMDN�����Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���BAD��130������B����D��90������E��F�ֱ����߶�BC��DC�ϵĶ��㣮����AEF���ܳ���Сʱ�����EAF�Ķ���Ϊ��������
A. 90��B. 80��C. 70��D. 60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
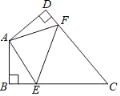
����Ŀ����ͼ���߳�Ϊ1��������ABCD�У�PΪ�Խ���AC�ϵ�����һ�㣬�ֱ�����PB��PD��PE��PB����CD��E��
��1����֤��PE=PD��
��2����EΪCD���е�ʱ����AP�ij���
��3����AP=x��0��x�� ![]() �����ı���BPEC�����Ϊy����֤��y=
�����ı���BPEC�����Ϊy����֤��y= ![]() ��
�� ![]() ��x��2 ��
��x��2 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��OAB�У���OBA=90�㣬�ҵ�B������Ϊ��0��4����
��1��д����A�����꣮
��2��������OAB�Ƶ�O˳ʱ����ת90���ġ�OA1B1��
��3�����A��ת����A1��������·�߳�����������У���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������![]() ֮��ı仯�����ͼ��ʾ������ͼ��ش��������⣮
֮��ı仯�����ͼ��ʾ������ͼ��ش��������⣮
(1)д��![]() �ı仯��Χ��
�ı仯��Χ��
(2)��![]() ʱ����
ʱ����![]() �Ķ�Ӧֵ��
�Ķ�Ӧֵ��
(3)��![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��ֵ���
��ֵ���
(4)��![]() ��ʲô��Χʱ��
��ʲô��Χʱ��![]() ��ֵ�ڲ������ӣ�
��ֵ�ڲ������ӣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com