练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列各式，属于二元一次方程的个数有（　　）

    ①xy+2x﹣y＝7；②4x+1＝x﹣y；③+y＝5；④x＝y；⑤x2﹣y2＝2；⑥6x﹣2y；⑦x+y+z＝1；⑧y（y﹣1）＝2x2﹣y2+xy

    A.1B.2C.3D.4

    【答案】B

    【解析】

    根据二元一次方程的定义对各式进行判断即可．

    ①xy+2x﹣y＝7属于二元二次方程，故错误；

    ②4x+1＝x﹣y、④x＝y属于二元一次方程，故正确；

    ③+y＝5是分式方程，故错误；

    ⑤x2﹣y2＝2属于二元二次方程，故错误；

    ⑥6x﹣2y不是方程，故错误；

    ⑦x+y+z＝1属于三元一次方程，故错误；

    ⑧y（y﹣1）＝2x2﹣y2+xy属于二元二次方程，故错误．

    综上所述，属于二元一次方程的个数有2个．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

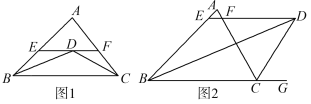
    【题目】(1)如图1，在△ABC中，BD，CD分别平分∠ABC，∠ACB，过点D作EF∥BC交AB，AC于点E，F，试说明BE＋CF＝EF的理由；

    (2)如图2，BD，CD分别平分∠ABC，∠ACG，过点D作EF∥BC交AB，AC于点E，F，则BE，CF，EF有怎样的数量关系？并说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】探究题．

    已知:如图．

    求证:

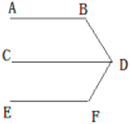
    老师要求学生在完成这道教材上的题目证明后，尝试对图形进行变式，继续做拓展探究，看看有什么新发现？

    （1）小颖首先完成了对这道题的证明，在证明过程中她用到了平行线的一条性质，小颖用到的平行线性质可能是_________．

    （2）接下来，小颖用《几何画板》对图形进行了变式，她先画了两条平行线然后在平行线间画了一点，连接后，用鼠标拖动点分别得到了图①②③，小颖发现图②正是上面题目的原型，于是她由上题的结论猜想到图①和③中的与之间也可能存在着某种数量关系于是她利用《几何画板》的度量与计算功能，找到了这三个角之间的数量关系．

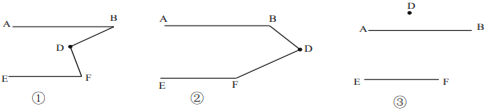
    请你在小颖操作探究的基础上，继续完成下面的问题：

    ①猜想图①中与之间的数量关系并加以证明：

    ②补全图③，直接写出与之间的数量关系：_______．

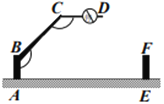
    （3）学以致用：一个小区大门栏杆的平面示意图如图所示，垂直地面于平行于地面

    ，若，则_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，BD是ABCD的对角线，AE⊥BD，CF⊥BD，垂足分别为E、F，求证：AE=CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，连结CE交AD于点F，连结BD交CE于点G，连结BE.下列结论：①CE＝BD；②△ADC是等腰直角三角形；③∠ADB＝∠AEB；④S四边形BCDE＝BD·CE；⑤BC2＋DE2＝BE2＋CD2.其中正确的结论有( )

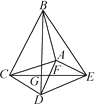
    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠1=∠2，∠B=∠C.求证：（1）AB∥CD;(2) ∠AEC=∠3.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点E、F是边长为4的正方形ABCD边AD、AB上的动点，且AF=DE，BE交CF于点P，在点E、F运动的过程中，PA的最小值为（ ）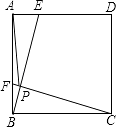
    A.2
    B.2
    C.4 ﹣2
    D.2 ﹣2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x、y的方程组 ，给出下列说法：
    ①当a=1时，方程组的解也是方程x+y=2的一个解；
    ②当x﹣2y＞8时，a＞ ；
    ③不论a取什么实数，2x+y的值始终不变；
    ④若y=x2+5，则a=﹣4． 以上说法正确的是（ ）
    A.②③④
    B.①②④
    C.③④
    D.②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点B在线段AC的延长线上，AC<CB,点M、N分别是AC、BC的中点，点D是AB的中点．

    （1）若AC=8cm,CB=10cm，求线段MN的长；

    （2）若AC=a,CB=b，求线段CD的长．

    查看答案和解析>>

    同步练习册答案