
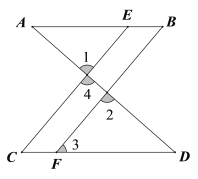
【题目】如图,已知∠1=∠2,∠B=∠C.求证:(1)AB∥CD;(2) ∠AEC=∠3.
【答案】(1)答案见详解,(2)答案见详解.
【解析】
(1)由∠1=∠2结合对顶角相等即可得出∠2=∠4,进而可证出CE∥BF,再根据平行线的性质可得出∠3=∠C=∠B,利用平行线的判定定理即可证出AB∥CD;
(2)由AB∥CD可得∠AEC=∠C,再根据(1)中∠B=∠C=∠3即可证得∠AEC=∠3.
证明:(1)∵∠1=∠2(已知),∠1=∠4(对顶角相等),
∴∠2=∠4(等量替换),
∴CE∥BF(同位角相等,两直线平行),
∴∠3=∠C(两直线平行,同位角相等).
又∵∠B=∠C(已知),
∴∠3=∠B(等量替换),
∴AB∥CD(内错角相等,两直线平行).
(2)∵AB∥CD(已知),
∴∠AEC=∠C(两直线平行,内错角相等).
∵∠B=∠C=∠3(由(1)可知),
∴∠AEC=∠3(等量替换).


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
【题目】如图所示,AB⊥BE于点B,DE⊥BE于点E.
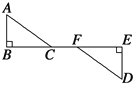
(1)若∠A=∠D,AB=DE,则△ABC与△DEF全等的理由是____;
(2)若∠A=∠D,BC=EF,则△ABC与△DEF全等的理由是_________;
(3)若AB=DE,BC=EF,则△ABC与△DEF全等的理由是_______;
(4)若AB=DE,AC=DF,则△ABC与△DEF全等的理由是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732, ![]() =1.732,
=1.732, ![]() =1.414)
=1.414)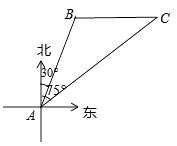
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式,属于二元一次方程的个数有( )
①xy+2x﹣y=7;②4x+1=x﹣y;③![]() +y=5;④x=y;⑤x2﹣y2=2;⑥6x﹣2y;⑦x+y+z=1;⑧y(y﹣1)=2x2﹣y2+xy
+y=5;④x=y;⑤x2﹣y2=2;⑥6x﹣2y;⑦x+y+z=1;⑧y(y﹣1)=2x2﹣y2+xy
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
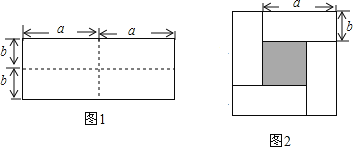
【题目】如图1是一个长为2a,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)写出图2的阴影部分的正方形的边长.
(2)用两种不同的方法求图中的阴影部分的面积.
(3)观察如图2,写出![]() 这三个代数式之间的等量关系.
这三个代数式之间的等量关系.
(4)根据(3)题中的等量关系,解决问题:若![]() 求
求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.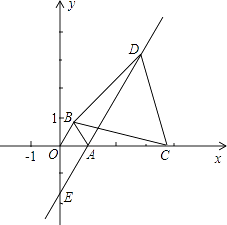
(1)如图,当C点在x轴上运动时,设AC=x,请用x表示线段AD的长;
(2)随着C点的变化,直线AE的位置变化吗?若变化,请说明理由;若不变,请求出直线AE的解析式.
(3)以线段BC为直径作圆,圆心为点F,当点C坐标为多少时直线EF∥直线BO?这时OF和直线BO的位置关系如何?请给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅、2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅,1个小餐厅,可供2280名学生就餐.
(1)求1个大餐厅,1个小餐厅分别可供多少名 就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从A地到B地的公路需经过C地,图中AC=6千米,∠CAB=15°,∠CBA=30°.因城市规划的需要,将在A,B两地之间修建一条笔直的公路.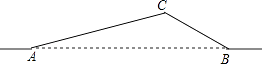
(1)求改直后的公路AB的长;
(2)问公路改直后该段路程比原来缩短了多少千米?(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com