
【题目】如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.

科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员中进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.

根据图中信息,回答下列问题:
(1)甲的平均数是___________,乙的中位数是______________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下面各题
①﹣40﹣28﹣(﹣19)+(﹣24)
②(﹣1![]() )×(﹣10)÷|﹣0.7|
)×(﹣10)÷|﹣0.7|
③﹣32﹣4×(﹣3)+15÷(﹣3)
④3x2﹣[7x﹣(4x﹣3)﹣2x2]
⑤5(a2b﹣3ab2)﹣2(a2b﹣7ab2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60 ![]() 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1: ![]() 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°=
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°= ![]() ,cos
,cos ![]() =
= ![]() ,tan53°=
,tan53°= ![]() ,
, ![]() ≈1.732,结果精确到0.1米)
≈1.732,结果精确到0.1米)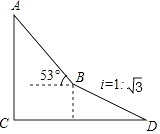
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题.
已知:如图![]() .
.
求证: ![]()
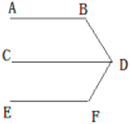
老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是_________.
(2)接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线![]() 然后在平行线间画了一点
然后在平行线间画了一点![]() ,连接
,连接![]() 后,用鼠标拖动点分
后,用鼠标拖动点分![]() 别得到了图①②③,小颖发现图②正是上面题目的原型,于是她由上题的结论猜想到图①和③中的
别得到了图①②③,小颖发现图②正是上面题目的原型,于是她由上题的结论猜想到图①和③中的![]() 与
与![]() 之间也可能存在着某种数量关系于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
之间也可能存在着某种数量关系于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
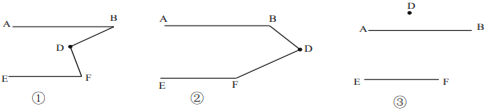
请你在小颖操作探究的基础上,继续完成下面的问题:
①猜想图①中![]() 与
与![]() 之间的数量关系并加以证明:
之间的数量关系并加以证明:
②补全图③,直接写出![]() 与
与![]() 之间的数量关系:_______.
之间的数量关系:_______.
(3)学以致用:一个小区大门栏杆的平面示意图如图所示,![]() 垂直地面
垂直地面![]() 于
于![]() 平行于地面
平行于地面
![]() ,若
,若![]() ,则
,则![]() _______.
_______.
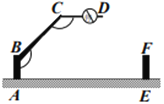
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明袋子中装有2个红球、1个黄球,这些球除颜色外都相同.小明搅匀后从中任意摸出一个球,记录颜色后放回、搅匀,再从中任意摸出1个球.则两次摸出的球都是黄球的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com