
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60 ![]() 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1: ![]() 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°=
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°= ![]() ,cos
,cos ![]() =
= ![]() ,tan53°=
,tan53°= ![]() ,
, ![]() ≈1.732,结果精确到0.1米)
≈1.732,结果精确到0.1米)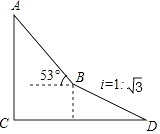
【答案】解:如图作BN⊥CD于N,BM⊥AC于M.
在Rt△BDN中,BD=30,BN:ND=1: ![]() ,
,
∴BN=15,DN=15 ![]() ,
,
∵∠C=∠CMB=∠CNB=90°,
∴四边形CMBN是矩形,
∴CM=BN=15,BM=CN=60 ![]() ﹣15
﹣15 ![]() =45
=45 ![]() ,
,
在Rt△ABM中,tan∠ABM= ![]() =
= ![]() ,
,
∴AM=60 ![]() ,
,
∴AC=AM+CM=15+60 ![]() .
.
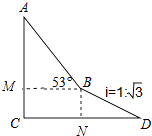
【解析】如图作BN⊥CD于N,BM⊥AC于M,先在RT△BDN中求出线段BN,在RT△ABM中求出AM,再证明四边形CMBN是矩形,得CM=BN即可解决问题.
【考点精析】本题主要考查了关于仰角俯角问题的相关知识点,需要掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】现有一块三角形的空地,其三边的长分别为20m,30m,40m,现要把它分成面积为2:3:4的三部分,分别种植不同的花草,请你设计一种方案,并简单说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB⊥BE于点B,DE⊥BE于点E.
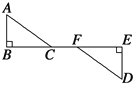
(1)若∠A=∠D,AB=DE,则△ABC与△DEF全等的理由是____;
(2)若∠A=∠D,BC=EF,则△ABC与△DEF全等的理由是_________;
(3)若AB=DE,BC=EF,则△ABC与△DEF全等的理由是_______;
(4)若AB=DE,AC=DF,则△ABC与△DEF全等的理由是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写推理理由:
已知:如图,D,F,E分别是BC,AC,AB上的点,DF∥AB,DE∥AC,

试说明∠EDF=∠A.
解:∵DF∥AB(已知),
∴∠A+∠AFD=180°(____________________).
∵DE∥AC(已知),
∴∠AFD+∠EDF=180°(____________________).
∴∠A=∠EDF(____________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于P,如果AP=2,则AC的长为( )
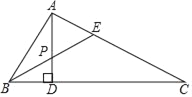
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
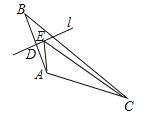
【题目】如图,在△ABC中,点D是AB边的中点,过点D作边AB的垂线l,E是l上任意一点,且AC=5,BC=8,则△AEC的周长最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732, ![]() =1.732,
=1.732, ![]() =1.414)
=1.414)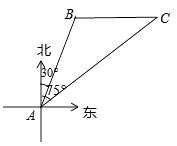
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅、2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅,1个小餐厅,可供2280名学生就餐.
(1)求1个大餐厅,1个小餐厅分别可供多少名 就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com