
【题目】一只不透明袋子中装有2个红球、1个黄球,这些球除颜色外都相同.小明搅匀后从中任意摸出一个球,记录颜色后放回、搅匀,再从中任意摸出1个球.则两次摸出的球都是黄球的概率是 .
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.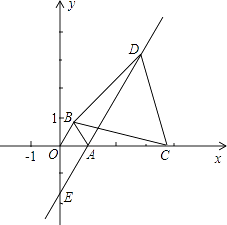
(1)如图,当C点在x轴上运动时,设AC=x,请用x表示线段AD的长;
(2)随着C点的变化,直线AE的位置变化吗?若变化,请说明理由;若不变,请求出直线AE的解析式.
(3)以线段BC为直径作圆,圆心为点F,当点C坐标为多少时直线EF∥直线BO?这时OF和直线BO的位置关系如何?请给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅、2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅,1个小餐厅,可供2280名学生就餐.
(1)求1个大餐厅,1个小餐厅分别可供多少名 就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个角的差的绝对值等于90°,就称这两个角互为垂角,其中一个角叫另一个角的垂角.
(1)如图1,O为直线AB上一点,∠AOC=90°,∠EOD=90°,直接写出图中∠BOE的垂角为 ;
(2)如果一个角的垂角等于这个角的补角的![]() ,求这个角的度数;
,求这个角的度数;
(3)如图2,O为直线AB上一点,∠AOC=75°,将整个图形绕点O逆时针旋转n°(0<n<180),直线AB旋转到A1B1,OC旋转到OC1,作射线OP,使∠BOP=![]() ∠BOB′,试直接写出当n= 时,∠POA1与∠AOC1互为垂角.
∠BOB′,试直接写出当n= 时,∠POA1与∠AOC1互为垂角.
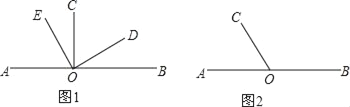
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若两个有理数a,b满足a+b=ab,则称a,b互为特征数.
(1)3与 互为特征数;
(2)正整数n (n>1)的特征数为 ;(用含n的式子表示)
(3)若m,n互为特征数,且m+mn=-2,n+mn=3,求m+n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从A地到B地的公路需经过C地,图中AC=6千米,∠CAB=15°,∠CBA=30°.因城市规划的需要,将在A,B两地之间修建一条笔直的公路.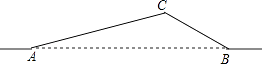
(1)求改直后的公路AB的长;
(2)问公路改直后该段路程比原来缩短了多少千米?(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com