
【题目】如果两个角的差的绝对值等于90°,就称这两个角互为垂角,其中一个角叫另一个角的垂角.
(1)如图1,O为直线AB上一点,∠AOC=90°,∠EOD=90°,直接写出图中∠BOE的垂角为 ;
(2)如果一个角的垂角等于这个角的补角的![]() ,求这个角的度数;
,求这个角的度数;
(3)如图2,O为直线AB上一点,∠AOC=75°,将整个图形绕点O逆时针旋转n°(0<n<180),直线AB旋转到A1B1,OC旋转到OC1,作射线OP,使∠BOP=![]() ∠BOB′,试直接写出当n= 时,∠POA1与∠AOC1互为垂角.
∠BOB′,试直接写出当n= 时,∠POA1与∠AOC1互为垂角.
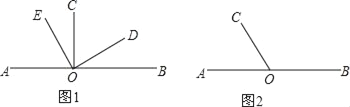
【答案】(1)∠DOB,∠EOC;(2)这个角的度数为18或126度;(3)30.
【解析】
(1)根据互为垂角的定义即可求解;
(2)利用题中的“一个角的垂角等于这个角的补角的![]() ”作为相等关系列方程求解;
”作为相等关系列方程求解;
(3)分0<n<75,75<n<90两种情况讨论可得n的值.
(1)∠EOB与∠DOB,∠EOB与∠EOC互为垂角的角,
∴图中∠BOE的垂角为∠DOB,∠EOC,
故答案为:∠DOB,∠EOC;
(2)设这个角的度数为x度,则
①当0<x<90时,它的垂角是90+x度,依题意有
90+x=![]() (180﹣x),
(180﹣x),
解得x=18;
②当90<x<180时,它的垂角是x﹣90度,依题意有
x﹣90=![]() (180﹣x),
(180﹣x),
解得x=126;
故这个角的度数为18或126度;
(3)当n=75时OC′和OA重合,分两种情况:
①当0<n<75时,∠COC′=n°,∠AOC′=75°﹣n°,
∠POB=![]() ∠BOB′=
∠BOB′=![]() n°,
n°,
∠A′OP=180°﹣(∠POB+∠BOB′)=180°﹣![]() n°,
n°,
∵∠A′OP﹣∠AOC′=90°,
∴|(180﹣![]() n)﹣(75﹣n)|=90,
n)﹣(75﹣n)|=90,
∵0<n<75,
∴n=30;
②当75<n<90时,∠AOC′=n°﹣75°,
∠POB=![]() ∠BOB′=
∠BOB′=![]() n°,
n°,
∠A′OP=180°﹣(∠POB+∠BOB′)=180°﹣![]() n°,
n°,
∵∠A′OP﹣∠AOC′=90°,
∴|(180﹣![]() n)﹣(n﹣75)|=90,
n)﹣(n﹣75)|=90,
解得n=66或138,
∵75<n<90,
∴n=66或138舍去;
综上所述;n=30时,∠POA′与∠AOC′互为垂角,
故答案为:30.


科目:初中数学 来源: 题型:
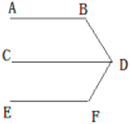
【题目】探究题.
已知:如图![]() .
.
求证: ![]()
老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是_________.
(2)接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线![]() 然后在平行线间画了一点
然后在平行线间画了一点![]() ,连接
,连接![]() 后,用鼠标拖动点分
后,用鼠标拖动点分![]() 别得到了图①②③,小颖发现图②正是上面题目的原型,于是她由上题的结论猜想到图①和③中的
别得到了图①②③,小颖发现图②正是上面题目的原型,于是她由上题的结论猜想到图①和③中的![]() 与
与![]() 之间也可能存在着某种数量关系于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
之间也可能存在着某种数量关系于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
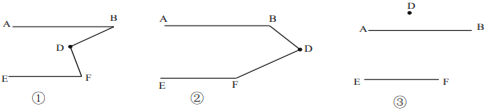
请你在小颖操作探究的基础上,继续完成下面的问题:
①猜想图①中![]() 与
与![]() 之间的数量关系并加以证明:
之间的数量关系并加以证明:
②补全图③,直接写出![]() 与
与![]() 之间的数量关系:_______.
之间的数量关系:_______.
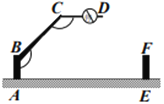
(3)学以致用:一个小区大门栏杆的平面示意图如图所示,![]() 垂直地面
垂直地面![]() 于
于![]() 平行于地面
平行于地面
![]() ,若
,若![]() ,则
,则![]() _______.
_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F是边长为4的正方形ABCD边AD、AB上的动点,且AF=DE,BE交CF于点P,在点E、F运动的过程中,PA的最小值为( ) 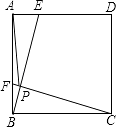
A.2
B.2 ![]()
C.4 ![]() ﹣2
﹣2
D.2 ![]() ﹣2
﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组 ![]() ,给出下列说法:
,给出下列说法:
①当a=1时,方程组的解也是方程x+y=2的一个解;
②当x﹣2y>8时,a> ![]() ;
;
③不论a取什么实数,2x+y的值始终不变;
④若y=x2+5,则a=﹣4. 以上说法正确的是( )
A.②③④
B.①②④
C.③④
D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
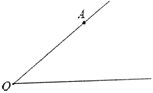
【题目】如图,点![]() 在
在![]() 的一边
的一边![]() 上,按要求画图并填空:
上,按要求画图并填空:
(1)过点![]() 画直线
画直线![]() ,与
,与![]() 的另一边相交于点
的另一边相交于点![]() ;
;
(2)过点![]() 画
画![]() 的垂线
的垂线![]() ,垂足为点
,垂足为点![]() ;
;
(3)过点![]() 画直线
画直线![]() ,交直线
,交直线![]() 于点
于点![]() ;
;
(4)直接写出![]() _____
_____![]() ;
;
(5)如果![]() ,
,![]() ,
,![]() ,那么点
,那么点![]() 到直线
到直线![]() 的距离为_______.
的距离为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明袋子中装有2个红球、1个黄球,这些球除颜色外都相同.小明搅匀后从中任意摸出一个球,记录颜色后放回、搅匀,再从中任意摸出1个球.则两次摸出的球都是黄球的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于点D,且BD=DC,E是BC延长线上一点,且点C在AE的垂直平分线上.有下列结论:
①AB=AC=CE;②AB+BD=DE;③AD=![]() AE;④BD=DC=CE.
AE;④BD=DC=CE.
其中,正确的结论是( )

A. 只有![]() B. 只有
B. 只有![]()
C. 只有![]() D. 只有
D. 只有![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC的延长线上,AC<CB,点M、N分别是AC、BC的中点,点D是AB的中点.
![]()
(1)若AC=8cm,CB=10cm,求线段MN的长;
(2)若AC=a,CB=b,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假设我市出租车收费标准是:起步价6元,可乘3千米;3千米到5千米,每千米1.6元;超过5千米,每千米2.4元.
(1)若某人乘坐的路程为4千米,那么他支付的费用是多少?
(2)若某人乘坐了x(x>5)千米的路程,则他应支付的费用是多少?
(3)若某人乘坐的路程为10千米,那么他应支付的费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com