
【题目】如图,从A地到B地的公路需经过C地,图中AC=6千米,∠CAB=15°,∠CBA=30°.因城市规划的需要,将在A,B两地之间修建一条笔直的公路.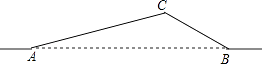
(1)求改直后的公路AB的长;
(2)问公路改直后该段路程比原来缩短了多少千米?(结果保留根号)
【答案】
(1)解:过点A作AD⊥BC交BC的延长线于点D,
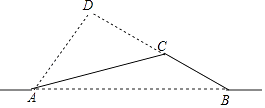
∵∠B=30°,∠CAB=15°,
∴∠ACD=45°.
在RtACD中,∠ADC=90°,∠ACD=45°,AC=6,
∴CD=AD=3 ![]() ,
,
在RtABD中,∠ADB=90°,∠B=30°,AD=3 ![]() ,
,
∴AB=6 ![]() ,
,
答:改直后的公路AB的长为6 ![]() 千米
千米
(2)解:在RtABD中,∠ADB=90°,∠B=30°,AD=3 ![]() ,
,
∴BD=3 ![]()
∴BC=3 ![]() ﹣3
﹣3 ![]() ,
,
AC+BC﹣AB=6+3 ![]() ﹣3
﹣3 ![]() ﹣6
﹣6 ![]()
=6+3 ![]() ﹣9
﹣9 ![]() (1分)
(1分)
答:公路改直后该段路程比原来缩短了(6+3 ![]() ﹣9
﹣9 ![]() )千米.
)千米.
【解析】(1)过点A作AD⊥BC交BC的延长线于点D,在RtACD中,∠ADC=90°,∠ACD=45°,AC=6,推出CD=AD=3 ![]() ,在RtABD中,∠ADB=90°,∠B=30°,AD=3
,在RtABD中,∠ADB=90°,∠B=30°,AD=3 ![]() ,推出AB=6
,推出AB=6 ![]() ,即可解决问题;(2)根据AC和BC的长度,即可得出公路改直后该段段路程比原来缩短的路程。
,即可解决问题;(2)根据AC和BC的长度,即可得出公路改直后该段段路程比原来缩短的路程。


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】一只不透明袋子中装有2个红球、1个黄球,这些球除颜色外都相同.小明搅匀后从中任意摸出一个球,记录颜色后放回、搅匀,再从中任意摸出1个球.则两次摸出的球都是黄球的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题|1﹣ ![]() |﹣
|﹣ ![]() +2cos30°﹣20170;
+2cos30°﹣20170;
(1)计算:|1﹣ ![]() |﹣
|﹣ ![]() +2cos30°﹣20170;
+2cos30°﹣20170;
(2)解不等式组 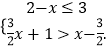 并求其最小整数解.
并求其最小整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC的延长线上,AC<CB,点M、N分别是AC、BC的中点,点D是AB的中点.
![]()
(1)若AC=8cm,CB=10cm,求线段MN的长;
(2)若AC=a,CB=b,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=a,直接写出∠DOE的度数(用含a的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置.
①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
②在∠AOC的内部有一条射线OF,且∠AOC-4∠AOF=2∠BOE+∠AOF,试确定∠AOF与∠DOE的度数之间的关系,说明理由.
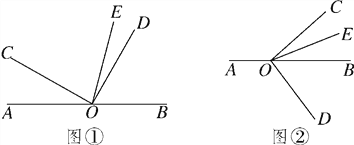
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )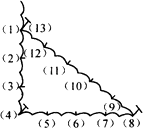
A.直角三角形两个锐角互补
B.三角形内角和等于180°
C.如果三角形两条边长的平方和等于第三边长的平方
D.如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
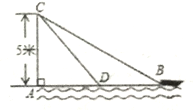
【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中的两点A(m,0),B(2m,0)(m>0),二次函数y=ax2+bx+m的图象与x轴交与A,B两点与y轴交于点C,顶点为点D.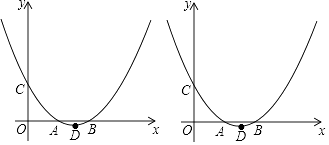
(1)当m=1时,直线BC的解析式为 , 二次函数y=ax2+bx+m的解析式为;
(2)求二次函数y=ax2+bx+m的解析式为(用含m的式子表示);
(3)连接AC、AD、BD,请你探究 ![]() 的值是否与m有关?若有关,求出它与m的关系;若无关,说明理由;
的值是否与m有关?若有关,求出它与m的关系;若无关,说明理由;
(4)当m为正整数时,依次得到点A1 , A2 , …,Am的横坐标分别为1,2,…m;点B1 , B2 , …,Bm 的横坐标分别为2,4,…2m(m≤10);经过点A1 , B1 , 点A2 , B2 , …,点Am , Bm的这组抛物线y=ax2+bx+m分别与y轴交于点C1 , C2 , …,Cm , 由此得到了一组直线B1C1 , B2C2 , …,BmCm , 在点B1 , B2 , …,Bm 中任取一点Bn , 以线段OBn为边向上作正方形OBnEnFn , 若点En在这组直线中的一条直线上,直接写出所有满足条件的点En的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com