
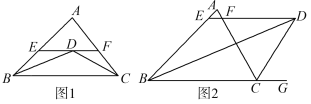
【题目】(1)如图1,在△ABC中,BD,CD分别平分∠ABC,∠ACB,过点D作EF∥BC交AB,AC于点E,F,试说明BE+CF=EF的理由;
(2)如图2,BD,CD分别平分∠ABC,∠ACG,过点D作EF∥BC交AB,AC于点E,F,则BE,CF,EF有怎样的数量关系?并说明你的理由.
【答案】(1)见解析;(2)BE-CF=EF,理由见解析
【解析】
(1)根据BD平分∠ABC,可得∠ABD=∠CDB,再利用EF∥BC,可证BE=ED和DF=CF,然后即可证明BE+CF=EF.
(2)由(1)知BE=ED,同理可得CF=DF,然后利用等量代换即可证明BE、CF、EF有怎样的数量关系.
解:(1)理由如下:∵BD平分∠ABC,∴∠ABD=∠CBD,∵EF∥BC,
∴∠EDB=∠DBC,∴∠ABD=∠EDB,∴BE=ED,同理DF=CF,∴BE+CF=EF.
(2)BE-CF=EF.理由如下:由(1)知BE=ED,∵EF∥BC,CD平分∠ACG,
∴∠EDC=∠DCG=∠ACD,∴CF=DF,又∵ED-DF=EF,∴BE-CF=EF.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB于D点,M,N是AC,BC上的动点,且∠MDN=90°,下列结论:①AM=CN;②四边形MDNC的面积为定值;③AM2+BN2=MN2;④NM平分∠CND.其中正确的是 ( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形可以看成是线段平移得到的图形,如图1,将线段AD沿AB的方向平移AB个单位至BC处,就可以得到平行四边形ABCD,或者将线段AB沿AD的方向平移AD个单位至DC处,也可以得到平行四边形ABCD.
(1)在图2,图3,图4中,给出平行四边形ABCD的顶点A,B,D的坐标,写出图2,图3,图4中的顶点C的坐标,它们分别是_____,_______,_______;
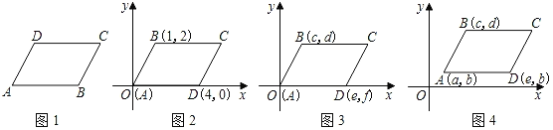
(2)通过对图2,3,4的观察和顶点C的坐标的探究,你会发现:无论平行四边形ABCD处于直角坐标系中哪个位置,当其顶点坐标为A(a,b),B(c,d),C(m,n),D(e,f)(如图5)时,则四个顶点的横坐标a,c,m,e之间的等量关系为______;纵坐标b,d,n,f之间的等量关系为_______(不必证明);
(3)如图6,在平面直角坐标系中,已知A(﹣3,0),B(3,0),C(2,4),则以A,B,C三个点为顶点的平行四边形的第四个顶点D的坐标为______.
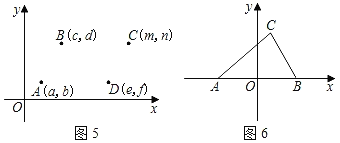
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已如点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2019个单位长度没有弹性的细线(线的相细忽略不计)的一端固定在A处,并按![]() 的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是__________.
的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )

A. ![]() B.
B. ![]() C. 5 D.
C. 5 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB⊥BE于点B,DE⊥BE于点E.
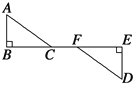
(1)若∠A=∠D,AB=DE,则△ABC与△DEF全等的理由是____;
(2)若∠A=∠D,BC=EF,则△ABC与△DEF全等的理由是_________;
(3)若AB=DE,BC=EF,则△ABC与△DEF全等的理由是_______;
(4)若AB=DE,AC=DF,则△ABC与△DEF全等的理由是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的个数是( )
①2a2﹣a2=a2;
② ![]() +
+ ![]() =2
=2 ![]() ;
;
③(π﹣3.14)0× ![]() =0;
=0;
④a2÷a× ![]() =a2;
=a2;
⑤sin30°+cos60°= ![]() ;
;
⑥精确到万位6295382≈6.30×106 .
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于P,如果AP=2,则AC的长为( )
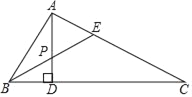
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式,属于二元一次方程的个数有( )
①xy+2x﹣y=7;②4x+1=x﹣y;③![]() +y=5;④x=y;⑤x2﹣y2=2;⑥6x﹣2y;⑦x+y+z=1;⑧y(y﹣1)=2x2﹣y2+xy
+y=5;④x=y;⑤x2﹣y2=2;⑥6x﹣2y;⑦x+y+z=1;⑧y(y﹣1)=2x2﹣y2+xy
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com