
ЁОЬтФПЁПЦНааЫФБпаЮПЩвдПДГЩЪЧЯпЖЮЦНвЦЕУЕНЕФЭМаЮЃЌШчЭМ1ЃЌНЋЯпЖЮADбиABЕФЗНЯђЦНвЦABИіЕЅЮЛжСBCДІЃЌОЭПЩвдЕУЕНЦНааЫФБпаЮABCDЃЌЛђепНЋЯпЖЮABбиADЕФЗНЯђЦНвЦADИіЕЅЮЛжСDCДІЃЌвВПЩвдЕУЕНЦНааЫФБпаЮABCDЃЎ
ЃЈ1ЃЉдкЭМ2ЃЌЭМ3ЃЌЭМ4жаЃЌИјГіЦНааЫФБпаЮABCDЕФЖЅЕуAЃЌBЃЌDЕФзјБъЃЌаДГіЭМ2ЃЌЭМ3ЃЌЭМ4жаЕФЖЅЕуCЕФзјБъЃЌЫќУЧЗжБ№ЪЧ_____ЃЌ_______ЃЌ_______ЃЛ
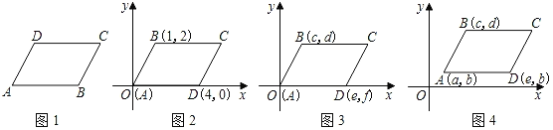
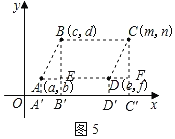
ЃЈ2ЃЉЭЈЙ§ЖдЭМ2ЃЌ3ЃЌ4ЕФЙлВьКЭЖЅЕуCЕФзјБъЕФЬНОПЃЌФуЛсЗЂЯжЃКЮоТлЦНааЫФБпаЮABCDДІгкжБНЧзјБъЯЕжаФФИіЮЛжУЃЌЕБЦфЖЅЕузјБъЮЊAЃЈaЃЌbЃЉЃЌBЃЈcЃЌdЃЉЃЌCЃЈmЃЌnЃЉЃЌDЃЈeЃЌfЃЉЃЈШчЭМ5ЃЉЪБЃЌдђЫФИіЖЅЕуЕФКсзјБъaЃЌcЃЌmЃЌeжЎМфЕФЕШСПЙиЯЕЮЊ______ЃЛзнзјБъbЃЌdЃЌnЃЌfжЎМфЕФЕШСПЙиЯЕЮЊ_______ЃЈВЛБижЄУїЃЉЃЛ
ЃЈ3ЃЉШчЭМ6ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊAЃЈЉ3ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌCЃЈ2ЃЌ4ЃЉЃЌдђвдAЃЌBЃЌCШ§ИіЕуЮЊЖЅЕуЕФЦНааЫФБпаЮЕФЕкЫФИіЖЅЕуDЕФзјБъЮЊ______ЃЎ
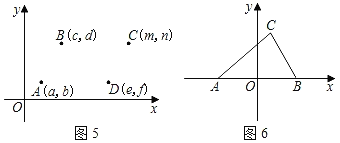
ЁОД№АИЁПЃЈ1ЃЉЃЈ5ЃЌ2ЃЉЃЌЃЈe+cЃЌdЃЉЃЌЃЈc+eЉaЃЌdЃЉЃЛЃЈ2ЃЉmЃНc+eЉaЃЛnЃНd+fЉbЃЛЃЈ3ЃЉЃЈ8ЃЌ4ЃЉЛђЃЈЉ2ЃЌЉ4ЃЉЛђЃЈЉ4ЃЌ4ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЦНааЫФБпаЮЕФаджЪЃКЖдБпЦНааЧвЯрЕШЃЌЧѓНтМДПЩЃЛ
ЃЈ2ЃЉШчЭМзїИЈжњЯпЃЌжЄУїЁїBEAЁеЁїCFDЃЈAASЃЉЃЌЭЦГіAEЃНDFЃНcЉaЃЌBEЃНCFЃНdЉbЃЌгжвбжЊCЕуЕФзјБъЮЊЃЈmЃЌnЃЉЃЌПЩЕУmЃНeЃЋcЉaЃЌnЃНdЉbЃЋfЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉЕФНсТлМДПЩЕУГіД№АИЃЎ
НтЃКЃЈ1ЃЉгЩЦНааЫФБпаЮЕФаджЪКЭЦНвЦЕФаджЪЕУЃКЭМ1ЁЂЭМ2ЃЌ3жаЖЅЕуCЕФзјБъЗжБ№ЪЧЃКЃЈ5ЃЌ2ЃЉЁЂЃЈe+cЃЌdЃЉЃЌЃЈc+eЉaЃЌdЃЉЃЌ
ЙЪД№АИЮЊЃКЃЈ5ЃЌ2ЃЉЁЂЃЈe+cЃЌdЃЉЃЌЃЈc+eЉaЃЌdЃЉЃЛ
ЃЈ2ЃЉЗжБ№Й§ЕуAЃЌBЃЌCЃЌDзїxжсЕФДЙЯпЃЌДЙзуЗжБ№ЮЊA'ЃЌB'ЃЌC'ЃЌD'ЃЌ
ЗжБ№Й§AЃЌDзїAEЁЭBB'гкEЃЌDFЁЭCC'гкЕуFЃЎ
дкЦНааЫФБпаЮABCDжаЃЌCDЃНBAЃЌCDЁЮBAЃЌ
Ёр![]() ЃЌ
ЃЌ
дкЁїBEAКЭЁїCFDжаЃЌ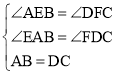 ЃЌ
ЃЌ
ЁрЁїBEAЁеЁїCFDЃЈAASЃЉЃЌ
дђAEЃНDFЃНcЉaЃЌBEЃНCFЃНdЉbЃЌ
ЁпCЕуЕФзјБъЮЊЃЈmЃЌnЃЉЃЌ
ЁрmЃНeЃЋcЉaЃЌnЃНdЉbЃЋfЃЌМДmЃНc+eЉaЃЛnЃНd+fЉb
ЙЪД№АИЮЊЃКmЃНc+eЉaЃЛnЃНd+fЉbЃЛ
ЃЈ3ЃЉЁпЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌAЃЈЉ3ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌCЃЈ2ЃЌ4ЃЉЃЌ
гЩЃЈ2ЃЉЕУЃКmЃНc+eЉaЃЛnЃНd+fЉbЃЌ
ЁрЕуDЕФзјБъЮЊЃЈ3+2+3ЃЌ0+4Љ0ЃЉЛђЃЈЉ3+3Љ2ЃЌ0+0Љ4ЃЉЛђЃЈЉ3+2Љ3ЃЌ0+4-0ЃЉЃЛ
МДЕуDзјБъЮЊЃЈ8ЃЌ4ЃЉЛђЃЈЉ2ЃЌЉ4ЃЉЛђЃЈЉ4ЃЌ4ЃЉЃЎ
ЙЪД№АИЮЊЃКЃЈ8ЃЌ4ЃЉЛђЃЈЉ2ЃЌЉ4ЃЉЛђЃЈЉ4ЃЌ4ЃЉЃЎ


 аЁбЇбЇЯАКУАяЪжЯЕСаД№АИ
аЁбЇбЇЯАКУАяЪжЯЕСаД№АИ аЁбЇЭЌВНШ§СЗКЫаФУмОэЯЕСаД№АИ
аЁбЇЭЌВНШ§СЗКЫаФУмОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЇЩњВњвЛжжЙЄОпЃЌОнЪаГЁЕїВщЃЌШєАДУПИіЙЄОп280дЊЯњЪлЪБЃЌУПдТПЩЯњЪл300ИіЃЌШєЯњЪлЕЅМлУПНЕЕЭ1дЊЃЌУПдТПЩЖрЪлГі2ИіЃЌОнЭГМЦЃЌУПИіЙЄОпЕФЙЬЖЈГЩБОQЃЈдЊЃЉгыдТЯњЪлyЃЈИіЃЉТњзуШчЯТЙиЯЕЃК
дТЯњСПyЃЈИіЃЉ | 100 | 160 | 240 | 320 |
УПИіЙЄОпЕФЙЬЖЈГЩБОQЃЈдЊЃЉ | 96 | 60 | 40 | 30 |
ЃЈ1ЃЉаДГідТВњЯњСПyЃЈИіЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓУПИіЭцОпЕФЙЬЖЈГЩБОQЃЈдЊЃЉгыдТВњЯњСПyЃЈИіЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉШєИУГЇетжжЭцОпЕФдТВњЯњСПВЛГЌЙ§400ИіЃЌдђУПИіЭцОпЕФЙЬЖЈГЩБОжСЩйЮЊЖрЩйдЊЃПЯњЪлЕЅМлзюЕЭЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁЯA=ЁЯAGEЃЌЁЯD=ЁЯDGCЃЎ
ЃЈ1ЃЉЪдЫЕУїABЁЮCDЃЛ
ЃЈ2ЃЉШєЁЯ1+ЁЯ2=180ЁуЃЌЧвЁЯBEC=2ЁЯB+60ЁуЃЌЧѓЁЯCЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
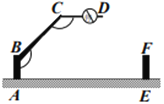
ЁОЬтФПЁПШчЭМЃЌЕуAЃЌBЃЌCЃЌDдкЭЌвЛЬѕжБЯпЩЯЃЌЕуEЃЌFЗжБ№дкжБЯпADЕФСНВрЃЌЧвAE=DFЃЌЁЯA=ЁЯDЃЌAB=DCЃЎ 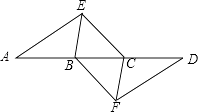
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮBFCEЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉШєAD=10ЃЌDC=3ЃЌЁЯEBD=60ЁуЃЌдђBE=ЪБЃЌЫФБпаЮBFCEЪЧСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНУћЩфЛїдЫЖЏдБжаНјааЩфЛїБШШќЃЌСНШЫдкЯрЭЌЬѕМўЯТИїЩфЛї10ДЮЃЌЩфЛїЕФГЩМЈШчЭМЫљЪО.

ИљОнЭМжааХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉМзЕФЦНОљЪ§ЪЧ___________ЃЌввЕФжаЮЛЪ§ЪЧ______________ЃЛ
ЃЈ2ЃЉЗжБ№МЦЫуМзЁЂввГЩМЈЕФЗНВюЃЌВЂДгМЦЫуНсЙћРДЗжЮіЃЌФуШЯЮЊФФЮЛдЫЖЏдБЕФЩфЛїГЩМЈИќЮШЖЈЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛзщЪ§Он6ЃЌ3ЃЌ4ЃЌ7ЃЌ6ЃЌ3ЃЌ5ЃЌ6ЃЌЧѓЃК
ЃЈ1ЃЉетзщЪ§ОнЕФЦНОљЪ§ЁЂжкЪ§ЁЂжаЮЛЪ§ЃЛ
ЃЈ2ЃЉетзщЪ§ОнЕФЗНВюКЭБъзМВю.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
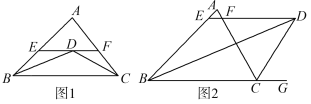
ЁОЬтФПЁП(1)ШчЭМ1ЃЌдкЁїABCжаЃЌBDЃЌCDЗжБ№ЦНЗжЁЯABCЃЌЁЯACBЃЌЙ§ЕуDзїEFЁЮBCНЛABЃЌACгкЕуEЃЌFЃЌЪдЫЕУїBEЃЋCFЃНEFЕФРэгЩЃЛ
(2)ШчЭМ2ЃЌBDЃЌCDЗжБ№ЦНЗжЁЯABCЃЌЁЯACGЃЌЙ§ЕуDзїEFЁЮBCНЛABЃЌACгкЕуEЃЌFЃЌдђBEЃЌCFЃЌEFгадѕбљЕФЪ§СПЙиЯЕЃПВЂЫЕУїФуЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЬНОПЬтЃЎ
вбжЊ:ШчЭМ![]() ЃЎ
ЃЎ
ЧѓжЄ: ![]()
РЯЪІвЊЧѓбЇЩњдкЭъГЩетЕРНЬВФЩЯЕФЬтФПжЄУїКѓЃЌГЂЪдЖдЭМаЮНјааБфЪНЃЌМЬајзіЭиеЙЬНОПЃЌПДПДгаЪВУДаТЗЂЯжЃП
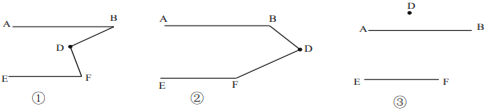
ЃЈ1ЃЉаЁгБЪзЯШЭъГЩСЫЖдетЕРЬтЕФжЄУїЃЌдкжЄУїЙ§ГЬжаЫ§гУЕНСЫЦНааЯпЕФвЛЬѕаджЪЃЌаЁгБгУЕНЕФЦНааЯпаджЪПЩФмЪЧ_________ЃЎ
ЃЈ2ЃЉНгЯТРДЃЌаЁгБгУЁЖМИКЮЛАхЁЗЖдЭМаЮНјааСЫБфЪНЃЌЫ§ЯШЛСЫСНЬѕЦНааЯп![]() ШЛКѓдкЦНааЯпМфЛСЫвЛЕу
ШЛКѓдкЦНааЯпМфЛСЫвЛЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() КѓЃЌгУЪѓБъЭЯЖЏЕуЗж
КѓЃЌгУЪѓБъЭЯЖЏЕуЗж![]() Б№ЕУЕНСЫЭМЂйЂкЂлЃЌаЁгБЗЂЯжЭМЂке§ЪЧЩЯУцЬтФПЕФдаЭЃЌгкЪЧЫ§гЩЩЯЬтЕФНсТлВТЯыЕНЭМЂйКЭЂлжаЕФ
Б№ЕУЕНСЫЭМЂйЂкЂлЃЌаЁгБЗЂЯжЭМЂке§ЪЧЩЯУцЬтФПЕФдаЭЃЌгкЪЧЫ§гЩЩЯЬтЕФНсТлВТЯыЕНЭМЂйКЭЂлжаЕФ![]() гы
гы![]() жЎМфвВПЩФмДцдкзХФГжжЪ§СПЙиЯЕгкЪЧЫ§РћгУЁЖМИКЮЛАхЁЗЕФЖШСПгыМЦЫуЙІФмЃЌевЕНСЫетШ§ИіНЧжЎМфЕФЪ§СПЙиЯЕЃЎ
жЎМфвВПЩФмДцдкзХФГжжЪ§СПЙиЯЕгкЪЧЫ§РћгУЁЖМИКЮЛАхЁЗЕФЖШСПгыМЦЫуЙІФмЃЌевЕНСЫетШ§ИіНЧжЎМфЕФЪ§СПЙиЯЕЃЎ
ЧыФудкаЁгБВйзїЬНОПЕФЛљДЁЩЯЃЌМЬајЭъГЩЯТУцЕФЮЪЬтЃК
ЂйВТЯыЭМЂйжа![]() гы
гы![]() жЎМфЕФЪ§СПЙиЯЕВЂМгвджЄУїЃК
жЎМфЕФЪ§СПЙиЯЕВЂМгвджЄУїЃК
ЂкВЙШЋЭМЂлЃЌжБНгаДГі![]() гы
гы![]() жЎМфЕФЪ§СПЙиЯЕЃК_______ЃЎ
жЎМфЕФЪ§СПЙиЯЕЃК_______ЃЎ
ЃЈ3ЃЉбЇвджТгУЃКвЛИіаЁЧјДѓУХРИИЫЕФЦНУцЪОвтЭМШчЭМЫљЪОЃЌ![]() ДЙжБЕиУц
ДЙжБЕиУц![]() гк
гк![]() ЦНаагкЕиУц
ЦНаагкЕиУц
![]() ЃЌШє
ЃЌШє![]() ЃЌдђ
ЃЌдђ![]() _______ЃЎ
_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com