
分析 首先求出不等式的解,再利用二次根式的除法运算法则化简求出即可.
解答 解:∵3x+5≤0,
∴x≤-$\frac{5}{3}$,
∵$\frac{4}{15}\sqrt{\frac{3y}{2x}}÷$M=$\frac{1}{2}\sqrt{\frac{xy}{2}}$,
∴M=$\frac{4}{15}$$\sqrt{\frac{3y}{2x}}$÷$\frac{1}{2}$$\sqrt{\frac{xy}{2}}$=$\frac{8}{15}$$\sqrt{\frac{3y}{2x}×\frac{2}{xy}}$=$\frac{8}{15}$$\sqrt{\frac{3}{{x}^{2}}}$=$\frac{8}{15}$×$\frac{3}{5}$$\sqrt{3}$=$\frac{8}{25}$$\sqrt{3}$.
点评 此题主要考查了二次根式的除法运算以及解不等式,熟练掌握二次根式的性质是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
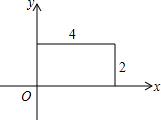 如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )
如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )| A. | (4,0) | B. | (2,4) | C. | (0,2) | D. | (4,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
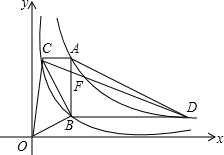 【问题情境】反比例函数y=$\frac{2}{x}$和y=$\frac{8}{x}$在平面直角坐标系xOy第一象限的图象如图所示,点A在y=$\frac{8}{x}$的图象上,AB∥y轴,与y=$\frac{2}{x}$的图象交于点B,AC、BD与x轴平行,分别与y=$\frac{2}{x}$、y=$\frac{8}{x}$的图象交于点C、D.点A、B、C、D的纵坐标分别记为yA、yB、yC、yD,记点A的横坐标为m(m>0).
【问题情境】反比例函数y=$\frac{2}{x}$和y=$\frac{8}{x}$在平面直角坐标系xOy第一象限的图象如图所示,点A在y=$\frac{8}{x}$的图象上,AB∥y轴,与y=$\frac{2}{x}$的图象交于点B,AC、BD与x轴平行,分别与y=$\frac{2}{x}$、y=$\frac{8}{x}$的图象交于点C、D.点A、B、C、D的纵坐标分别记为yA、yB、yC、yD,记点A的横坐标为m(m>0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
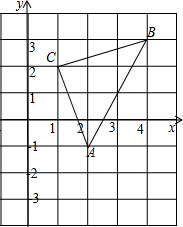 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知△ABC三个顶点的坐标分别是 A(-3,-1)、B(1,3)、C(2,-3)
已知△ABC三个顶点的坐标分别是 A(-3,-1)、B(1,3)、C(2,-3)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
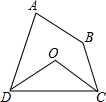 如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线交于点O,则∠COD的度数为( )
如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线交于点O,则∠COD的度数为( )| A. | 135° | B. | 120° | C. | 110° | D. | 100° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com