
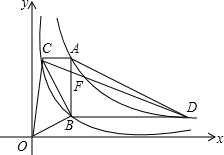
 【问题情境】反比例函数y=$\frac{2}{x}$和y=$\frac{8}{x}$在平面直角坐标系xOy第一象限的图象如图所示,点A在y=$\frac{8}{x}$的图象上,AB∥y轴,与y=$\frac{2}{x}$的图象交于点B,AC、BD与x轴平行,分别与y=$\frac{2}{x}$、y=$\frac{8}{x}$的图象交于点C、D.点A、B、C、D的纵坐标分别记为yA、yB、yC、yD,记点A的横坐标为m(m>0).
【问题情境】反比例函数y=$\frac{2}{x}$和y=$\frac{8}{x}$在平面直角坐标系xOy第一象限的图象如图所示,点A在y=$\frac{8}{x}$的图象上,AB∥y轴,与y=$\frac{2}{x}$的图象交于点B,AC、BD与x轴平行,分别与y=$\frac{2}{x}$、y=$\frac{8}{x}$的图象交于点C、D.点A、B、C、D的纵坐标分别记为yA、yB、yC、yD,记点A的横坐标为m(m>0).分析 特例探究:根据函数与自变量的对应关系,可得A、B、C、D的坐标,根据三角形的面积公式,可得答案;
归纳:根据梯形的面积公式,可得答案;
拓展应用:根据图形的割补法,可得答案;根据相似三角形的性质,可得答案.
解答 解:m=1时,yA=8,A(1,8)
yB=2,B(1,2),
AB=8-2=6;
yC=8,xC=$\frac{1}{4}$,C($\frac{1}{4}$,8),
AC=1-$\frac{1}{4}$=$\frac{3}{4}$.
S△ABC=$\frac{1}{2}$×6×$\frac{3}{4}$=$\frac{9}{4}$,
当m=2时,yC=yA=4,A(2,4),
yB=1,B(2,1),AB=4-1=3,
xD=8,D(8,1),BD=8-2=6,
S△ABD=$\frac{1}{2}$AB•BD=$\frac{1}{2}$×3×6=9,
归纳:任意m(m>0),猜想梯形的面积的大小不发生变化,
A(m,$\frac{8}{m}$),C($\frac{m}{4}$,$\frac{8}{m}$),AC=$\frac{3}{4}$m,
B(m,$\frac{2}{m}$),D(4m,$\frac{2}{m}$),AB=$\frac{6}{m}$,BD=3m,
S梯形ACBD=$\frac{1}{2}$(AC+BD)•AB=$\frac{1}{2}$($\frac{3}{4}$m+3m)•$\frac{6}{m}$=$\frac{45}{4}$,
拓展应用:延长CB交x轴于E点,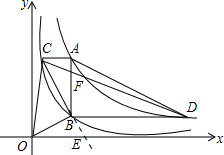
BC的解析式为y=-$\frac{8}{{m}^{2}}$x+$\frac{10}{m}$,
E($\frac{5}{4}$m,0),
S△OBC=S△OCE-S△OBE=$\frac{1}{2}$×$\frac{5}{4}$m×$\frac{6}{m}$=$\frac{15}{4}$;
△ACF∽△BDF,
S△AFC:S△BDF=(AC:BD)2=[($\frac{3}{4}$m):(3m)]2=1:16,
故答案为:8,$\frac{9}{4}$,;4,9;1:16.
点评 本题考查了反比例函数综合题,利用自变量与函数值的对应关系得出A、B、C、D点的坐标,又利用三角形的面积公式得出答案,图形的割补法是求面积的重要方法,相似三角形的判定与性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
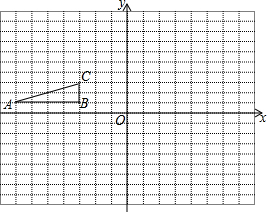 如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-7,1),点B的坐标为(-3,1),点C的坐标为(-3,3).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-7,1),点B的坐标为(-3,1),点C的坐标为(-3,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
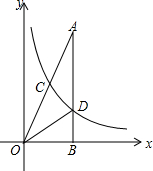 如图,在Rt△AOB中∠ABO=90°,点B在x轴上,点C(1,m)为OA的中点,一反比例函数的图象经过点C,交AB于点D.
如图,在Rt△AOB中∠ABO=90°,点B在x轴上,点C(1,m)为OA的中点,一反比例函数的图象经过点C,交AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
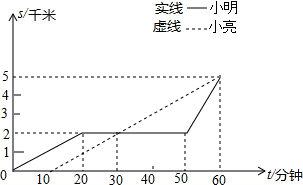 小明与小亮从学校出发到距学校5千米的图书馆看书,下图反应了他们两人离开学校的路程与时间的关系.据图回答以下问题:
小明与小亮从学校出发到距学校5千米的图书馆看书,下图反应了他们两人离开学校的路程与时间的关系.据图回答以下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com