
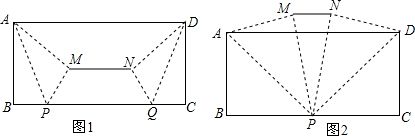
分析 (1)首先证明△ABP≌△DCQ,则∠APB=∠DQG,然后证明△MEP≌△NPQ即可证得;
(2)证明△EMP∽△MAG,根据相似三角形的对应边的比相等,以及矩形的性质即可求解;
(3)设PM、PN分别交AD于点E、F,证明△PEF∽△PMN,根据相似三角形的对应边的比相等即可求解.
解答 解:(1)①∵四边形ABCD是矩形,
∴∠B=∠C=90°,AB=CD.
∵在△ABP和△DCQ中,
$\left\{\begin{array}{l}{AB=DC}\\{∠B=∠C}\\{BP=CQ}\end{array}\right.$,
∴△ABP≌△DCQ,
∴∠APB=∠DQG.
∴∠MPE=180°-2∠APB=180°-2∠DQC=∠NQF.
∴在△MEP和△NPQ中,$\left\{\begin{array}{l}{∠MPE=∠NQF}\\{∠MEP=∠NPQ}\\{MP=NQ}\end{array}\right.$,
∴△MEP≌△NPQ,
∴ME=NF;
②∵ME∥NF,ME=NF,
∴四边形EFMN是矩形,
∴MN∥BC.
(2)延长EM、FN交AD于点G、H.
∵AB=4,BP=3,
∴AM=4,PM=3.
∵AD∥BC,
∴EM⊥AD.
∵∠AMP=∠MEP=∠MGA,
∴∠EMP=∠MAG.
∴△EMP∽△MAG.
∴$\frac{AG}{EM}=\frac{MG}{EP}=\frac{AM}{MP}=\frac{4}{3}$,
设AG=4a,MG=3b.
∵四边形ABEG是矩形,
∴$\left\{\begin{array}{l}{4a=3b+3}\\{3a+4b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{24}{25}}\\{b=\frac{7}{25}}\end{array}\right.$,
∴AG=$\frac{96}{25}$,同理DH=$\frac{96}{25}$.
∴MN=$\frac{108}{25}$;
(3)设PM、PN分别交AD于点E、F.
∵∠EPA=∠APB=∠PAE,
∴EA=EP.
设EA=EP=x,
在直角△AME中,42+(6-x)2=x2,
解得:x=$\frac{13}{9}$.
∴EF=12-2×$\frac{13}{3}$=$\frac{10}{3}$.
∵EF∥MN,
∴△PEF∽△PMN.
∴$\frac{EF}{MN}=\frac{PE}{PM}$,即$\frac{\frac{10}{3}}{MN}=\frac{\frac{13}{3}}{6}$,
解得:MN=$\frac{60}{13}$.
点评 本题考查了图形的折叠,以及全等三角形的判定与性质和相似三角形的判定与性质,注意在求线段的长时常用的方法是利用相似和解直角三角形.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
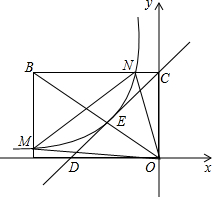 如图,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=2OC,直线y=x+b过点C,并且交对角线OB于点E,交x轴于点D,反比例函数y=$\frac{a}{x}$过点E且交AB于点M,交BC于点N,连接MN、OM、ON,若△OMN的面积是$\frac{80}{9}$,则a+b=1.
如图,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=2OC,直线y=x+b过点C,并且交对角线OB于点E,交x轴于点D,反比例函数y=$\frac{a}{x}$过点E且交AB于点M,交BC于点N,连接MN、OM、ON,若△OMN的面积是$\frac{80}{9}$,则a+b=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
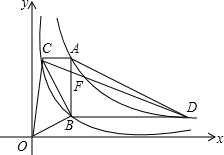 【问题情境】反比例函数y=$\frac{2}{x}$和y=$\frac{8}{x}$在平面直角坐标系xOy第一象限的图象如图所示,点A在y=$\frac{8}{x}$的图象上,AB∥y轴,与y=$\frac{2}{x}$的图象交于点B,AC、BD与x轴平行,分别与y=$\frac{2}{x}$、y=$\frac{8}{x}$的图象交于点C、D.点A、B、C、D的纵坐标分别记为yA、yB、yC、yD,记点A的横坐标为m(m>0).
【问题情境】反比例函数y=$\frac{2}{x}$和y=$\frac{8}{x}$在平面直角坐标系xOy第一象限的图象如图所示,点A在y=$\frac{8}{x}$的图象上,AB∥y轴,与y=$\frac{2}{x}$的图象交于点B,AC、BD与x轴平行,分别与y=$\frac{2}{x}$、y=$\frac{8}{x}$的图象交于点C、D.点A、B、C、D的纵坐标分别记为yA、yB、yC、yD,记点A的横坐标为m(m>0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com