练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．若m（m≠0）是方程x2-2x-mn=0的根，则m-n=2．

    分析 根据一元二次方程的解的定义得到m2-2m-mn=0，然后把等式两边除以m即可得到m-n的值．

    解答 解：根据题意得m2-2m-mn=0，
    而m≠0，
    所以m-2-n=0，
    所以m-n=2．
    故答案为2．

    点评 本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．又因为只含有一个未知数的方程的解也叫做这个方程的根，所以，一元二次方程的解也称为一元二次方程的根．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    20．化简分式：$\frac{x-2}{{x}^{2}+x-6}$=$\frac{1}{x+3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．【提出问题】如图1，小东将一张AD为12，宽AB为4的长方形纸片按如下方式进行折叠：在纸片的一边BC上分别取点P、Q，使得BP=CQ，连结AP、DQ，将△ABP、△DCQ分别沿AP、DQ折叠得△APM，△DQN，连结MN．小东发现线段MN的位置和长度随着点P、Q的位置发生改变．
    【规律探索】
    （1）请在图1中过点M，N分别画ME⊥BC于点E，NF⊥BC于点F．
    求证：①ME=NF；②MN∥BC．
    【解决问题】
    （2）如图1，若BP=3，求线段MN的长；
    （3）如图2，当点P与点Q重合时，求MN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

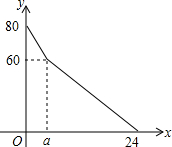    18．超市开设了自助收银区，实施自助收银，以节省顾客的排队时间．某日上午10点，超市值班经理发现在自助收银区已经有80人在等待收银，此时仍有顾客不断前来排队等候．在自助收银区，假设顾客按固定的速度增加，每个收银口自助收银的速度也是固定的，其中每分钟新增排队人数为3人，每分钟每个收银口自助收银2人．
    （1）若10点后收银的前a分钟只开放4个收银口，10点后排队等候的人数y（人）与收银时间x（分钟）的关系如图所示．
    ①求a值；
    ②求超市在10点20分时，自助收银区排队等候收银的顾客人数；
    （2）超市有承诺：顾客排队不超过10分钟，即要在10点10分内让所有排队的顾客都能完成自助收银，以便后来的顾客能随到随收．请帮助值班经理计算一下开放几个收银口？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．先化简，再求值：$\frac{a-3}{3{a}^{2}-6a}$÷（a+2-$\frac{5}{a-2}$），其中a是方程x2+3x-1=0的解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列因式分解正确的是（　　）
    A．x2-2x-1=（x-1）2B．2x2-2=2（x+1）（x-1）C．x2y-xy=y（x2-x）D．x2-2x+2=（x-1）2+1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．一件由黄金与白银制成的首饰重a g，商家称其中黄金含量不低于90%，黄金与白银的密度分别是19.3g/cm3与10.5g/cm3，列出不等式表示这件首饰的体积应满足什么条件．（提示：质量=密度×体积）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．已知点A、B坐标分别为（0，2）和（3，0），则AB=$\sqrt{13}$（保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

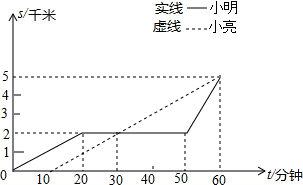    3．小明与小亮从学校出发到距学校5千米的图书馆看书，下图反应了他们两人离开学校的路程与时间的关系．据图回答以下问题：
    （1）小明与小亮谁先出发？先出发几分钟？
    答：小明出发；先出发10分钟．
    （2）小明前20分钟的速度是6千米/小时；
    小明最后10分钟的速度是18千米/小时．
    （3）小明与小亮从学校到图书馆的平均速度各是多少？

    查看答案和解析>>

    同步练习册答案