
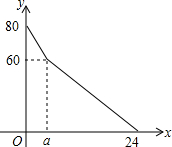
 超市开设了自助收银区,实施自助收银,以节省顾客的排队时间.某日上午10点,超市值班经理发现在自助收银区已经有80人在等待收银,此时仍有顾客不断前来排队等候.在自助收银区,假设顾客按固定的速度增加,每个收银口自助收银的速度也是固定的,其中每分钟新增排队人数为3人,每分钟每个收银口自助收银2人.
超市开设了自助收银区,实施自助收银,以节省顾客的排队时间.某日上午10点,超市值班经理发现在自助收银区已经有80人在等待收银,此时仍有顾客不断前来排队等候.在自助收银区,假设顾客按固定的速度增加,每个收银口自助收银的速度也是固定的,其中每分钟新增排队人数为3人,每分钟每个收银口自助收银2人.分析 (1)根据原有的人数-a分钟检票额人数+a分钟增加的人数=60建立方程求出其解就可以;
(2)设当4≤x≤24时,y与x之间的函数关系式为y=kx+b,由待定系数法求出函数的解析式,再将x=20代入解析式就可以求出结论;
(3)设需同时开放n个检票口,根据原来的人数+10分进站人数≤n个检票口10分钟检票人数建立不等式,求出其解即可.
解答 解:(1)由图象知,80+3a-4×2a=60,
∴a=4;
(2)设当4≤x≤24时,y与x之间的函数关系式为y=kx+b,由题意得:
$\left\{\begin{array}{l}{4k+b=0}\\{24k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-3}\\{b=72}\end{array}\right.$,
∴y=-3x+72,
当x=20时,y=-3×20+72=12,
即超市在10点20分时,自助收银区排队等候收银的顾客人数为12人.
(3)设需同时开放n个检票口,则由题意知
2a×10≥80+10×3,
解得:n≥$\frac{11}{2}$,
∵n为整数,
∴n的最小值为6.
答:至少需要同时开放6个检票口.
点评 本题考查了待定系数法求一次函数的解析式的运用,一元一次不等式的运用,解答的过程中求出函数的解析式是关键,建立一元一次不等式是重点.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
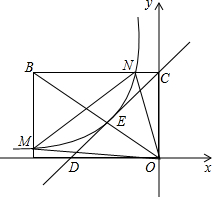 如图,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=2OC,直线y=x+b过点C,并且交对角线OB于点E,交x轴于点D,反比例函数y=$\frac{a}{x}$过点E且交AB于点M,交BC于点N,连接MN、OM、ON,若△OMN的面积是$\frac{80}{9}$,则a+b=1.
如图,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=2OC,直线y=x+b过点C,并且交对角线OB于点E,交x轴于点D,反比例函数y=$\frac{a}{x}$过点E且交AB于点M,交BC于点N,连接MN、OM、ON,若△OMN的面积是$\frac{80}{9}$,则a+b=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
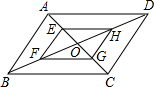 如图,在?ABCD中,对角线AC与BD相交于点O,点E,F,G,H分别在AO,BO,CO,DO上.
如图,在?ABCD中,对角线AC与BD相交于点O,点E,F,G,H分别在AO,BO,CO,DO上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象经过点A(1,4),B(m,n).
在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象经过点A(1,4),B(m,n).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知△ABC三个顶点的坐标分别是 A(-3,-1)、B(1,3)、C(2,-3)
已知△ABC三个顶点的坐标分别是 A(-3,-1)、B(1,3)、C(2,-3)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com