
 在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象经过点A(1,4),B(m,n).
在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象经过点A(1,4),B(m,n).分析 (1)将点A的坐标代入反比例函数求出k,再将点B的坐标代入计算即可;
(2)把mn的值代入,再根据二次函数图象上点的坐标特征表示出n,然后代入整理即可得解;
(3)先求出反比例函数与直线的交点坐标,再根据二次函数图象上点的坐标特征列不等式计算即可得解.
解答 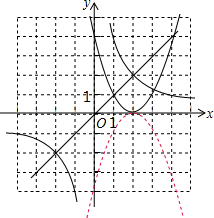 解:(1)将A(1,4)代入y=$\frac{k}{x}$得,k=1×4=4,
解:(1)将A(1,4)代入y=$\frac{k}{x}$得,k=1×4=4,
所以,反比例函数解析式为y=$\frac{4}{x}$,
将点B的坐标代入得$\frac{4}{m}$=n,
所以mn=4;
(2)∵二次函数y=(x-1)2的图象经过点B,
∴n=(m-1)2=m2-2m+1,
又∵mn=4,
∴m3n-2m2n+3mn-4n=4m2-8m+12-4(m2-2m+1)=4m2-8m+12-4m2+8m-4=8;
(3)联立$\left\{\begin{array}{l}{y=x}\\{y=\frac{4}{x}}\end{array}\right.$解得$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=-2}\end{array}\right.$,
所以,反比例函数图象与直线y=x的交点坐标为(2,2)(-2,-2),
∵反比例函数与抛物线的交点在直线下方,
∴抛物线开口向上时,a(2-1)2<2,
解得a<2,
∴0<a<2,
抛物线开口向下时,a(-2-1)2<-2,
解得a<-$\frac{2}{9}$,
综上所述,a的取值范围是0<a<2或a<-$\frac{2}{9}$.
点评 本题考查了二次函数与不等式,反比例函数图象上点的坐标特征,二次函数图象上点的坐标特征,难点在于(3)先求出反比例函数图象与直线的交点坐标.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 30和115 | B. | 30和105 | C. | 20和100 | D. | 15和105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
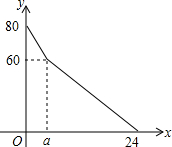 超市开设了自助收银区,实施自助收银,以节省顾客的排队时间.某日上午10点,超市值班经理发现在自助收银区已经有80人在等待收银,此时仍有顾客不断前来排队等候.在自助收银区,假设顾客按固定的速度增加,每个收银口自助收银的速度也是固定的,其中每分钟新增排队人数为3人,每分钟每个收银口自助收银2人.
超市开设了自助收银区,实施自助收银,以节省顾客的排队时间.某日上午10点,超市值班经理发现在自助收银区已经有80人在等待收银,此时仍有顾客不断前来排队等候.在自助收银区,假设顾客按固定的速度增加,每个收银口自助收银的速度也是固定的,其中每分钟新增排队人数为3人,每分钟每个收银口自助收银2人.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-2x-1=(x-1)2 | B. | 2x2-2=2(x+1)(x-1) | C. | x2y-xy=y(x2-x) | D. | x2-2x+2=(x-1)2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
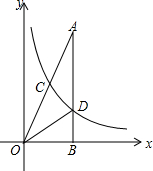 如图,在Rt△AOB中∠ABO=90°,点B在x轴上,点C(1,m)为OA的中点,一反比例函数的图象经过点C,交AB于点D.
如图,在Rt△AOB中∠ABO=90°,点B在x轴上,点C(1,m)为OA的中点,一反比例函数的图象经过点C,交AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.3×108 | B. | 1.3×109 | C. | 1.3×1010 | D. | 13×109 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com