
分析 根据质量=密度×体积,表示出当黄金含量为90%时V的取值范围,进而得出答案.
解答 解:设首饰的体积为V立方厘米,得:
$\frac{0.9a}{19.3}$+$\frac{0.1a}{10.5}$≥V
化简得:a($\frac{9}{193}$+$\frac{1}{105}$)≥V
解得:V≤$\frac{1138}{20265}$a,
故这件首饰的体积应满足的条件为:$\frac{a}{19.3}$≤V≤$\frac{1138}{20265}$a,即:$\frac{10a}{193}$≤V≤$\frac{1138}{20265}$a.
点评 此题主要考查了由实际问题抽象出一元一次不等式,表示出V的最大值是解题关键.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象经过点A(1,4),B(m,n).
在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象经过点A(1,4),B(m,n).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
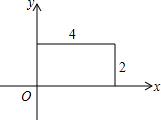 如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )
如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )| A. | (4,0) | B. | (2,4) | C. | (0,2) | D. | (4,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
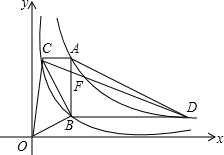 【问题情境】反比例函数y=$\frac{2}{x}$和y=$\frac{8}{x}$在平面直角坐标系xOy第一象限的图象如图所示,点A在y=$\frac{8}{x}$的图象上,AB∥y轴,与y=$\frac{2}{x}$的图象交于点B,AC、BD与x轴平行,分别与y=$\frac{2}{x}$、y=$\frac{8}{x}$的图象交于点C、D.点A、B、C、D的纵坐标分别记为yA、yB、yC、yD,记点A的横坐标为m(m>0).
【问题情境】反比例函数y=$\frac{2}{x}$和y=$\frac{8}{x}$在平面直角坐标系xOy第一象限的图象如图所示,点A在y=$\frac{8}{x}$的图象上,AB∥y轴,与y=$\frac{2}{x}$的图象交于点B,AC、BD与x轴平行,分别与y=$\frac{2}{x}$、y=$\frac{8}{x}$的图象交于点C、D.点A、B、C、D的纵坐标分别记为yA、yB、yC、yD,记点A的横坐标为m(m>0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com