
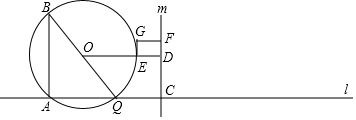
分析 (1)由已知得出AQ=3t,由三角函数求出AB=4t,再由勾股定理求出BQ=$\sqrt{A{B}^{2}+A{Q}^{2}}$=5t,作OM⊥AQ于M,则AM=QM=$\frac{1}{2}$AQ=1.5t,CD=OM,由三角形中位线定理得出CD=OM=$\frac{1}{2}$AB=2t,得出DF=$\frac{1}{3}$CD=$\frac{2}{3}$t;
(2)设矩形DEGF的面积为S,求出OE=$\frac{5}{2}$t,OD=QM+CQ=$\frac{3}{2}$t+1,得出DE=OD-OE=1-t,由矩形面积得出S是t的二次函数,即可得出答案;
(3)当矩形DEGF为正方形时,则DE=DF,分两种情况:①当0<t<1时,得出方程,解方程即可;
②当t≥1时,DE=t-1,得出方程,解方程即可.
解答 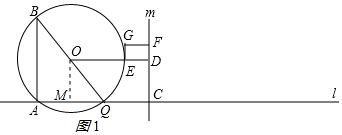 解:(1)∵点Q沿着直线l以3厘米/秒的速度由点A向右运动,运动时间为t秒.
解:(1)∵点Q沿着直线l以3厘米/秒的速度由点A向右运动,运动时间为t秒.
∴AQ=3t,
∵∠BAQ=90°,tan∠ABQ=$\frac{AQ}{AB}$=$\frac{3}{4}$,
∴AB=4t,
∴BQ=$\sqrt{A{B}^{2}+A{Q}^{2}}$=5t,
作OM⊥AQ于M,则AM=QM=$\frac{1}{2}$AQ=1.5t,CD=OM,
∴OM是△ABQ的中位线,
∴CD=OM=$\frac{1}{2}$AB=2t,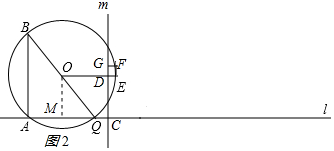
∴DF=$\frac{1}{3}$CD=$\frac{2}{3}$t;
(2)设矩形DEGF的面积为S,
∵OE=OB=$\frac{1}{2}$BQ=$\frac{5}{2}$t,OD=QM+CQ=$\frac{3}{2}$t+1,
∴DE=OD-OE=$\frac{3}{2}$t+1-$\frac{5}{2}$t=1-t,
∴$S=DF•DE=\frac{2}{3}t(1-t)=-\frac{2}{3}{(t-\frac{1}{2})^2}+\frac{1}{6}$,
∴当t=$\frac{1}{2}$时,矩形DEGF的最大面积为$\frac{1}{6}$;
(3)当矩形DEGF为正方形时,则DE=DF,分两种情况:
①当0<t<1时,如图1所示:DE=1-t,
∴1-t=$\frac{2}{3}$t,
解得:t=$\frac{3}{5}$;
②当t≥1时,如图2所示:DE=t-1,
∴t-1=$\frac{2}{3}$t,
解得:t=3;
综上所述:当矩形DEGF为正方形时,t的值为$\frac{3}{5}$或3.
点评 本题是圆的综合题目,考查了垂径定理、三角函数、勾股定理、矩形的面积、二次函数的最值、正方形的性质等知识;本题综合性强,有一定难度.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
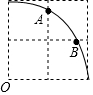 在2×2的正方形网格中,每个小正方形的边长为1.以点O为圆心,2为半径画弧交图中网格线与点A,B,则弧AB的长是$\frac{π}{3}$.
在2×2的正方形网格中,每个小正方形的边长为1.以点O为圆心,2为半径画弧交图中网格线与点A,B,则弧AB的长是$\frac{π}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
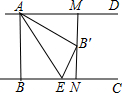 如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M、N,当点MB′=$\frac{1}{3}$MN时,BE的长为$\frac{3\sqrt{2}}{2}$.
如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M、N,当点MB′=$\frac{1}{3}$MN时,BE的长为$\frac{3\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
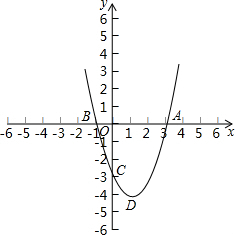 如图,在平面直角坐标系中,二次函数y=x2+bx+c的对称轴为经过点(1,0)的直线,其图象与x轴交于点A、B,且过点C(0,-3),其顶点为D.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的对称轴为经过点(1,0)的直线,其图象与x轴交于点A、B,且过点C(0,-3),其顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
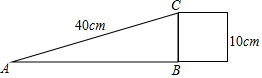 为了方便行人推车过某天桥,市政府在10m高的天桥一侧修建了40m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )
为了方便行人推车过某天桥,市政府在10m高的天桥一侧修建了40m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图表示下列四个不等式组中其中一个的解集,这个不等式组是( )
如图表示下列四个不等式组中其中一个的解集,这个不等式组是( )| A. | $\left\{\begin{array}{l}{x≥2}\\{x>-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x≤2}\\{x<-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x≥2}\\{x<-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x≤2}\\{x>-3}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com