
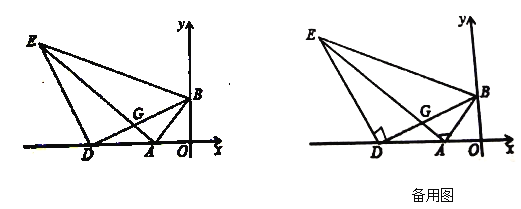
【题目】如图1,![]() ,
,![]() ,满足:
,满足:![]() .
.![]() .
.
(1)![]() ______;
______;
(2)点![]() 是
是![]() 点左侧的
点左侧的![]() 轴上一点,连接
轴上一点,连接![]() ,以
,以![]() 为直角边作等腰直角
为直角边作等腰直角![]() ,
,![]() .连接
.连接![]() ,
,![]() 交
交![]() 于点
于点![]() ;
;
①求![]() .
.
②若![]() 平分
平分![]() ,试求
,试求![]() 的长.
的长.
【答案】(1)![]() ;(2)①90°;②
;(2)①90°;②![]()
【解析】
(1)根据题意得出![]() ,求出b=4.得出a+b=0.a=-4,即可得出A、B的坐标,由勾股定理可得AB的长;
,求出b=4.得出a+b=0.a=-4,即可得出A、B的坐标,由勾股定理可得AB的长;
(2)①过点E作EH⊥x轴于点H,由AAS证明△EHD≌△DOB,得出DH=OB=OA=4,EH=OD.证出EH=AH.得出△EHA为等腰直角三角形.由等腰直角三角形的性质得出∠EAH=45°=∠BAO.得出∠EAB=90°即可;
②延长BA、ED相交于点H,由ASA证明△BEA≌△HEA,得出HA=BA=4![]() .得出BH=2AB=8
.得出BH=2AB=8![]() .证出∠DEG=∠DBH.由ASA证明△EDG≌△BDH,得出EG=BH=8
.证出∠DEG=∠DBH.由ASA证明△EDG≌△BDH,得出EG=BH=8![]() 即可.
即可.
(1)∵![]() ,
,
∴![]()
解得:b=4.
此时![]() ,
,
∴a+b=0.
∴a=-4,
∴A(-4,0)、B(0,4).
∴AB=![]() ;
;
(2)①如图1,过点E作EH⊥x轴于点H.则∠EDH+∠DEH=90°.

∵∠EDB=90°.
∴∠EDH+∠BDO=90°.
∴∠BDO=∠DEH.
在△EHD和△DOB中,
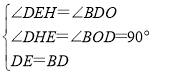
∴△EHD≌△DOB.
∴DH=OB=OA=4,EH=OD.
而AH=DH+AD=OA+AD=OD.
∴EH=AH.
∴△EHA为等腰直角三角形.
∴∠EAH=45°=∠BAO.
∴∠EAB=90°.
②如图2,延长BA、ED相交于点Q.

∵EA平分∠BEQ.
∴∠QEA=∠BEA.
由①得:∠EAB=90°=∠EAQ.
在△BEA和△QEA中,
 ,
,
∴△BEA≌△QEA.
∴QA=BA=![]() .
.
∴BQ=2AB=8![]() .
.
∵∠EDG=90°=∠GAB.且∠EGD=∠BGA.
∴∠DEG=∠DBQ.
在△EDG和△BDQ中,
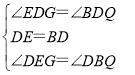
∴△EDG≌△BDH(ASA).
∴EG=BH=8![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线相交于点A1,得∠A1;∠A1BC和∠A1CD的平分线相交于点A2,得∠A2;…;∠A2018BC和∠A2018CD的平分线交于点A2019,则∠A2019=________度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=5cm,BC=3cm,AC=4cm,若动点P从点C开始,按C→A→B的路径运动,且速度为每秒2cm,设出发的时间为t秒
(1)请判断△ABC的形状,说明理由.
(2)当t= 时,△BCP是以BC为腰的等腰三角形.
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒1cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,P、Q两点之间的距离为![]() ?
?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若BC=4,CD=6,求平行四边形OABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,恒有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”,同理函数y=x也是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=![]() 是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
(2)如果已知二次函数y=x2﹣4x+k是闭区间[2,t]上的“闭函数”,求k和t的值;
(3)如果(2)所述的二次函数的图象交y轴于C点,A为此二次函数图象的顶点,B为直线x=1上的一点,当△ABC为直角三角形时,写出点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论是________.(写出正确命题的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.
(1)当D点在BC的什么位置时,DE=DF?请说明理由.
(2)DE,DF,CG的长之间存在着怎样的等量关系?并说明理由.
(3)若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定两数a,b之间的一种运算,记作(a,b):如果![]() ,那么(a,b)=c.
,那么(a,b)=c.
例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
(3,9)=_____,(5,125)=_____,(![]() ,
,![]() )=_____,(-2,-32)=_____.
)=_____,(-2,-32)=_____.
(2)令![]() ,
,![]() ,
,![]() ,试说明下列等式成立的理由:
,试说明下列等式成立的理由:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少;
(4)如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com