
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若BC=4,CD=6,求平行四边形OABC的面积.

【答案】(1)证明见解析(2)24
【解析】试题分析:(1)连接OD,求出∠EOC=∠DOC,根据SAS推出△EOC≌△DOC,推出∠ODC=∠OEC=90°,根据切线的判定推出即可;
(2)根据切线长定理求出CE=CD=4,根据平行四边形性质求出OA=OD=4,根据平行四边形的面积公式=2△COD的面积即可求解.
试题解析:(1)证明:连接OD,
∵OD=OA,
∴∠ODA=∠A,
∵四边形OABC是平行四边形,
∴OC∥AB,
∴∠EOC=∠A,∠COD=∠ODA,
∴∠EOC=∠DOC,
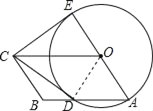
在△EOC和△DOC中,
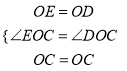
∴△EOC≌△DOC(SAS),
∴∠ODC=∠OEC=90°,
即OD⊥DC,
∴CD是⊙O的切线;
(2)由(1)知CD是圆O的切线,
∴△CDO为直角三角形,
∵S△CDO=![]() CDOD,
CDOD,
又∵OA=BC=OD=4,
∴S△CDO=![]() ×6×4=12,
×6×4=12,
∴平行四边形OABC的面积S=2S△CDO=24.


科目:初中数学 来源: 题型:
【题目】如图![]() ,在平面直角坐标系中,抛物线
,在平面直角坐标系中,抛物线![]() 经过
经过![]() 、
、![]() 两点,与x轴交于另一点C,顶点为D.
两点,与x轴交于另一点C,顶点为D.
![]() 求该抛物线的解析式及点C、D的坐标;
求该抛物线的解析式及点C、D的坐标;
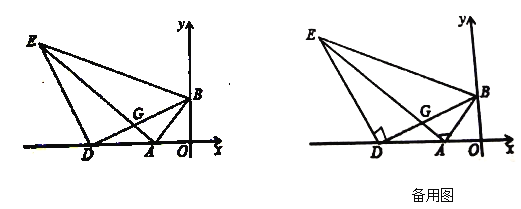
![]() 经过点B、D两点的直线与x轴交于点E,若点F是抛物线上一点,以A、B、E、F为顶点的四边形是平行四边形,求点F的坐标;
经过点B、D两点的直线与x轴交于点E,若点F是抛物线上一点,以A、B、E、F为顶点的四边形是平行四边形,求点F的坐标;
![]() 如图
如图![]() 是抛物线上的点,Q是直线AP上方的抛物线上一动点,求
是抛物线上的点,Q是直线AP上方的抛物线上一动点,求![]() 的最大面积和此时Q点的坐标.
的最大面积和此时Q点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,半圆O的直径AB=10cm,弦AC=6cm,将半圆沿着过点A的直线折叠,折叠后使得弦AC恰好落在直径AB上,则折痕AD的长为_______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某校田径队25人年龄的平均数和中位数都是16岁,但是后来发现其中有一位同学的年龄登记错误,将17岁写成了19岁,经重新计算后,正确的平均数为a岁,中位数为b岁,则下列结论中正确的是( )
A. a>16,b=16 B. a>16,b<16 C. a<16,b<16 D. a<16,b=16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年某企业按餐厨垃圾处理费25元/吨,建筑垃圾处理费16元/吨标准,共支付餐厨和建筑垃圾处理费5200元,从2014年元月起,收费标准上调为:餐厨垃圾处理费100元/吨,建筑垃圾处理费30元/吨,若该企业2014年处理的这两种垃圾数量与2013年相比没有变化,就要多支付垃圾处理费8800元,
(1)该企业2013年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2014年将上述两种垃圾处理量减少到240吨,且建筑垃圾处理费不超过餐厨垃圾处理量的3倍,则2014年该企业最少需要支付这两种垃圾处理费共多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() ,
,![]() ,满足:
,满足:![]() .
.![]() .
.
(1)![]() ______;
______;
(2)点![]() 是
是![]() 点左侧的
点左侧的![]() 轴上一点,连接
轴上一点,连接![]() ,以
,以![]() 为直角边作等腰直角
为直角边作等腰直角![]() ,
,![]() .连接
.连接![]() ,
,![]() 交
交![]() 于点
于点![]() ;
;
①求![]() .
.
②若![]() 平分
平分![]() ,试求
,试求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,AB BC AC,∠A ∠B ∠C 60°.点 D、E 分别是边 AC、AB 上的点(不与 A、B、C 重合),点 P 是平面内一动点.设∠PDC=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点 P 在边 BC 上运动(不与点 B 和点 C 重合),如图⑴所示,则∠1+∠2 .(用 α 的代数式表示)
(2)若点 P 在△ABC 的外部,如图⑵所示,则∠α、∠1、∠2 之间有何关系?写出你的结论,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com