【题目】已知等腰三角形的两边分别为6和3，则此等腰三角形周长为____；已知等腰三角形的一个内角为50°，则它的顶角为____．
【答案】15 50°或80°
【解析】
空1：有两种情况（6是腰和3是腰），先依据三角形的三边关系判断能否构成三角形，若能计算周长；
空2：有两种情况（顶角是50°和底角是50°时），由等边对等角求出底角的度数，用三角形的内角和定理即可求出顶角的度数．
解：空1：因为等腰三角形的两边长分别为6和3.
当三边长为3、3、6时，
∵3+3=6
所以不能构成三角形，
当三边长为3、6、6时，能构成三角形，其周长为6+6+3=15；
空2：如图所示，△ABC中，AB=AC.
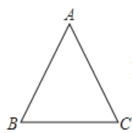
有两种情况：
①顶角∠A=50°；
②当底角是50°时，
∵AB=AC，
∴∠B=∠C=50°，
∵∠A+∠B+∠C=180°，
∴∠A=180°50°50°=80°
∴这个等腰三角形的顶角为50°和80°.
故本题第一个空填：15，第二个空填：50°和80°.
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】投资1万元围一个矩形菜园(如图)，其中一边靠墙，另外三边选用不同材料建造.墙长24 m，平行于墙的边的费用为200元/m，垂直于墙的边的费用为150元/m，设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m，直接写出y与x之间的函数关系式；
(2)若菜园面积为384 m2，求x的值；
(3)求菜园的最大面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（题文）如图，AB是
的直径，且
，点M为外一点，且MA，MC分别切于点A、C两点
与AM的延长线交于点D．
求证：
；
填空
当
______时，四边形AOCM是正方形．
当______时，
为等边三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
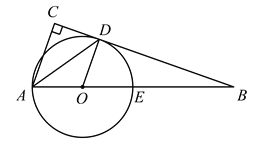
【题目】如图，在Rt△ABC中，∠ACB=90°，AD平分∠BAC交BC于点D，点O是AB边上一点，以O为圆心作⊙O且经过A，D两点，交AB于点E．
（1）求证：BC是⊙O的切线；
（2）AC=2，AB=6，求BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了解某校九年级学生的理化实验操作情况，随机抽查了40名同学实验操作的得分．根据获取的样本数据，制作了如下的条形统计图和扇形统计图．请根据相关信息，解答下列问题：
（Ⅰ）扇形 ①的圆心角的大小是 ；
（Ⅱ）求这40个样本数据的平均数、众数、中位数；
（Ⅲ）若该校九年级共有320名学生，估计该校理化实验操作得满分（10分）有多少人．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平行四边形ABCD中，
，
，
绕点C旋转，角的两边分别与AB、AD交于点E、F，同时也分别与DA、BA的延长线交于点G、H．
如图1，若
．
求证：
≌
；
在绕点C旋转的过程中，线段AC、AG、AH之间存在着怎样的数量关系？并说明理由．
如图2，若
，经探究得
的值为常数k，求k的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料：
在数学课上，老师提出利用尺规作图完成下面问题：
已知：∠ACB是△ABC的一个内角．
求作：∠APB=∠ACB．
小明的做法如下：
如图
①作线段AB的垂直平分线m；
②作线段BC的垂直平分线n，与直线m交于点O；
③以点O为圆心，OA为半径作△ABC的外接圆；
④在弧ACB上取一点P，连结AP，BP．
所以∠APB=∠ACB．
老师说：“小明的作法正确．”
请回答：
（1）点O为△ABC外接圆圆心（即OA=OB=OC）的依据是_____；
（2）∠APB=∠ACB的依据是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
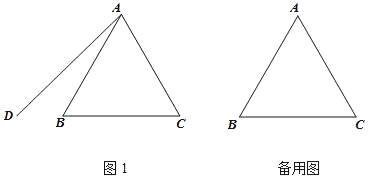
【题目】在等边△ABC外作射线AD，使得AD和AC在直线AB的两侧，∠BAD=α（0°＜α＜180°），点B关于直线AD的对称点为P，连接PB，PC．
（1）依题意补全图1；
（2）在图1中，求△BPC的度数；
（3）直接写出使得△PBC是等腰三角形的α的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法中，错误的是（ ）
A.在直角三角形ABC中，已知两边长为3和4，则第三边长一定为5；
B.三角形的三边a、b、c满足a2+b2=c2，则∠C=90°；
C.△ABC中，若∠A：∠B：∠C=1：2：3，则△ABC是直角三角形；
D.△ABC中，若a：b：c=3：4：5，则这个三角形是直角三角形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com