
【题目】我们知道三角形任意两条中线的交点是三角形的重心.重心有如下性质:重心到顶点的距离是重心到对边中点距离的2倍,请利用该性质解决问题:
(1)如图1,在![]() 中,
中,![]() 、
、![]() 是中线,
是中线,![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() ,
,![]() ;
;
(2)如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 是中线,
是中线,![]() 于点
于点![]() ,猜想
,猜想![]() 、
、![]() 、
、![]() 三者之间的关系并证明;
三者之间的关系并证明;
(3)如图2,在![]() 中,点
中,点![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .求AF的长.
.求AF的长.

【答案】(1)1,![]() ;(2)a2+b2=5c2;(3)AF=4.
;(2)a2+b2=5c2;(3)AF=4.
【解析】
(1)由三角形的重心定理得出BP=2EP=2,AP=2FP,得出EP=1,由直角三角形的性质得出AP=![]() BP=2
BP=2![]() ,即可得出FP=
,即可得出FP=![]() AP=
AP=![]()
(2)设PF=m,PE=n,由![]() =
=![]() =
=![]() ,得到AP=2m,PB=2n,再由勾股定理即可得出结论;
,得到AP=2m,PB=2n,再由勾股定理即可得出结论;
(3)连接AC、EC,由平行四边形的性质得出AD=BC,AD∥BC,证明四边形AFCE是平行四边形,得出AF=CE,由平行线得出△AEQ∽△CBQ,得出![]() =
=![]() =
=![]() =
=![]() ,设AQ=a,EQ=b,则CQ=2a,BQ=2b,证明EG是△ACD的中位线,由三角形中位线定理得出EG∥AC,得出BE⊥AC,由勾股定理得得出方程,求出a2=
,设AQ=a,EQ=b,则CQ=2a,BQ=2b,证明EG是△ACD的中位线,由三角形中位线定理得出EG∥AC,得出BE⊥AC,由勾股定理得得出方程,求出a2=![]() ,得出BQ2=4b2=
,得出BQ2=4b2=![]() ,b2=
,b2=![]() ,在Rt△EQC中,由勾股定理求出CE,即可得出AF的长.
,在Rt△EQC中,由勾股定理求出CE,即可得出AF的长.
解:(1)∵在△ABC中,AF、BE是中线,
∴BP=2EP=2,AP=2FP,
∴EP=1,
∵AF⊥BE,∠FAB=30°,![]()
![]()
故答案为:1,![]()
(2)a2+b2=5c2;理由如下:
连接EF,如图1所示:
∵AF,BE是△ABC的中线,
∴EF是△ABC的中位线,
∴EF∥AB,且![]() AB=
AB=![]() c,
c,
∴![]() =
=![]() =
=![]() ,,
,,
设PF=m,PE=n,
∴AP=2m,PB=2n,
在Rt△APB中,(2m)2+(2n)2=c2,即4m2+4n2=c2,
在Rt△APE中,(2m)2+n2=(![]() b)2,即4m2+n2=
b)2,即4m2+n2=![]() b2,
b2,
在Rt△FPB中,m2+(2n)2=(![]() a)2,即m2+4n2=
a)2,即m2+4n2=![]() a2,
a2,
∴5m2+5n2=![]() (a2+b2)=
(a2+b2)=![]() c2,
c2,
∴a2+b2=5c2;
(3)连接AC、EC,如图2所示:
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵点E,F分别是AD,BC,CD的中点,
∴AE=CE,
∴四边形AFCE是平行四边形,
∴AF=CE,
∵AD∥BC,
∴△AEQ∽△CBQ,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
设AQ=a,EQ=b,则CQ=2a,BQ=2b,
∵点E,G分别是AD,CD的中点,
∴EG是△ACD的中位线,
∴EG∥AC,
∵BE⊥EG,
∴BE⊥AC,
由勾股定理得:AB2-AQ2=BC2-CQ2,
即9-a2=(2![]() )2-4a2,
)2-4a2,
∴3a2=11,
∴a2=![]() ,
,
∴BQ2=4b2=(2![]() )2-4×
)2-4×![]() =
=![]() ,
,
∴b2=![]() ×
×![]() =
=![]() ,
,
在Rt△EQC中,CE2=EQ2+CQ2=b2+4a2=16,
∴CE=4,
∴AF=4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.

(1)求证:四边形DEGF是平行四边形;
(2)当点G是BC的中点时,求证:四边形DEGF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校学生对A《最强大脑》、B《朗读者》、C《中国诗词大会》、D《出彩中国人》四个电视节目的喜爱情况,随机抽取了m学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),将调查结果绘制成如下两幅不完整的统计图(如图1和图2):
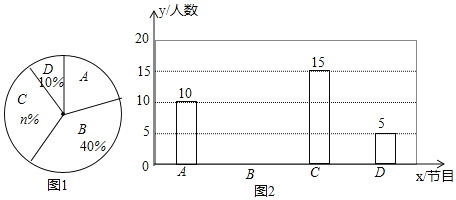
根据统计图提供的信息,回答下列问题;
(1)m= ,n= ;
(2)扇形统计图中,喜爱《最强大脑》节目所对应的扇形的圆心角度数是 度.
(3)根据以上信息直接在答题卡中补全条形统计图;
(4)根据抽样调查结果,请你估计该校6000名学生中有多少学生最喜欢《中国诗词大会》节目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,3辆大货车与4辆小货车一次可以运货27吨,2辆大货车与6辆小货车一次可以运货28吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨;
(2)目前有45吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,其中每辆大货车一次运货费用150元,每辆小货车一次运货费用100元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(﹣1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(﹣2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第124次跳动至A124的坐标( )

A.(63,62)B.(62,61)C.(﹣62,61)D.(124,123)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com