
【题目】如图,在ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAE=∠AEB.
∵AE是角平分线,
∴∠DAE=∠BAE.
∴∠BAE=∠AEB.
∴AB=BE.
同理AB=AF.
∴AF=BE.
∴四边形ABEF是平行四边形.
∵AB=BE,
∴四边形ABEF是菱形.
(2)解:作PH⊥AD于H,
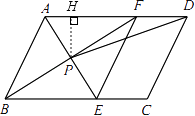
∵四边形ABEF是菱形,∠ABC=60°,AB=4,
∴AB=AF=4,∠ABF=∠AFB=30°,AP⊥BF,
∴AP= ![]() AB=2,
AB=2,
∴PH= ![]() ,DH=5,
,DH=5,
∴tan∠ADP= ![]() =
= ![]() .
.
【解析】(1)根据平行四边形的性质及角平分线的定义先证明出四边形ABEF是平行四边形.再根据一组邻边相等得平行四边形是菱形得出结论;(2)作PH⊥AD于H,根据菱形的性质得出AB=AF=4,∠ABF=∠AFB=30°,AP⊥BF,从而得出PH,DH的长度,根据正切函数的定义得出结论。


科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.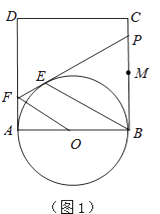
(1)求证:OF∥BE;
(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(3)延长DC、FP交于点G,连接OE并延长交直线DC于H(图2),问是否存在点P,使△EFO∽△EHG(E、F、O与E、H、G为对应点)?如果存在,试求(2)中x和y的值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(2,1),B(2,4).
(1)若直线l:y=x+b与AB有一个交点.

则b的取值范围为_______________;
(2)若直线l:y=kx与AB有一个交点.
则k的取值范围为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到县城城南大道的距离为100米的点P处.这时,一辆出租车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO=45°.
(1)求A、B之间的路程;
(2)请判断此出租车是否超过了城南大道每小时60千米的限制速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚为调查某校七年级学生对某一节目的了解程度,用简单随机抽样的办法抽取了该年级的一个班进行调查统计.A:熟悉,B:了解较多,C:一般了解.图1和图2是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求该班共有多少名学生.
(2)在条形图中,将表示“一般了解”的部分补充完整.
(3)如果全年级共400名同学,请你估算全年级对这一节目“了解较多”的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.
(1)求证:BD=CE;
(2)若BE、CD交于点F,求证:△BDF≌△CEF;
(3)在(2)的条件下连接AF,求证:AF平分∠BAC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道三角形任意两条中线的交点是三角形的重心.重心有如下性质:重心到顶点的距离是重心到对边中点距离的2倍,请利用该性质解决问题:
(1)如图1,在![]() 中,
中,![]() 、
、![]() 是中线,
是中线,![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() ,
,![]() ;
;
(2)如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 是中线,
是中线,![]() 于点
于点![]() ,猜想
,猜想![]() 、
、![]() 、
、![]() 三者之间的关系并证明;
三者之间的关系并证明;
(3)如图2,在![]() 中,点
中,点![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .求AF的长.
.求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①![]() ;②
;②![]() ;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定.由统计图可知正确的结论是( )
;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定.由统计图可知正确的结论是( )

A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com