
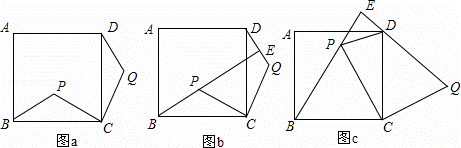
如图,点P是正方形ABCD 内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接B
内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接B P,DQ.
P,DQ.
(1)如图a,求证:△BCP≌△DCQ;
(2)如图,延长BP交直线DQ于点E.
 ①如图b,求证:BE⊥DQ;
①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判 断△DEP的形状,并说明理由.
断△DEP的形状,并说明理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.如max{﹣3,2}=2.
(1)max{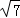 ,3}= 3 ;
,3}= 3 ;
(2)已知y1=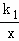 和y2=k2x+b在同一坐标系中的图象如图所示,若max{
和y2=k2x+b在同一坐标系中的图象如图所示,若max{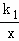 ,k2x+b}=
,k2x+b}=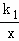 ,结合图象,直接写出x的取值范围;
,结合图象,直接写出x的取值范围;
(3)用分类讨论的方法,求max{2x+1,x﹣2}的值.
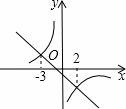
查看答案和解析>>
科目:初中数学 来源: 题型:
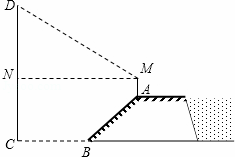
如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1: (指坡面的铅直高度与水平宽度的比),且AB=20m.身高为1.7m的小明站在大堤A点,测得髙压电线杆顶端点D的仰角为30°.已知地面CB宽30m,求髙压电线杆CD的髙度(结果保留三个有效数字,
(指坡面的铅直高度与水平宽度的比),且AB=20m.身高为1.7m的小明站在大堤A点,测得髙压电线杆顶端点D的仰角为30°.已知地面CB宽30m,求髙压电线杆CD的髙度(结果保留三个有效数字, ≈1.732).
≈1.732).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com