
 如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )
如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )| A. | 25海里 | B. | 30海里 | C. | 40海里 | D. | 50海里 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 锐角弯 | B. | 钝角弯 | C. | 直角弯 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,5) | B. | (5,2) | C. | (2,-5) | D. | (5,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,∠B=∠B′ | B. | $\frac{AB}{A′C′}$=$\frac{A′B′}{AC}$,∠B=∠B′ | ||
| C. | $\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,∠A=∠A′ | D. | $\frac{AB}{A′B′}$=$\frac{AC}{B′C′}$,∠A=∠A′ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
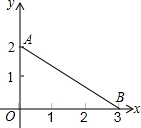 如图,线段AB对应的函数表达式为( )
如图,线段AB对应的函数表达式为( )| A. | y=-$\frac{3}{2}$x+2 | B. | y=-$\frac{2}{3}$x+2 | C. | y=-$\frac{2}{3}$x+2(0≤x≤3) | D. | y=-$\frac{2}{3}$x+20(0<x<3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 分数/分 | 120 | 110 | 100 | 90 | 80 | 70 |
| 人数/人 | 7 | 14 | 17 | 8 | 2 | 2 |
| A. | 98分 | B. | 100分 | C. | 102分 | D. | 104分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 建立直角坐标系,描出下列各点A(-2,2),B(-1,0),C(0,2)
建立直角坐标系,描出下列各点A(-2,2),B(-1,0),C(0,2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com