练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，四边形ABCD中，点M ， N分别在AB ， BC上，将△BMN沿MN翻折，得△FMN ， 若MF∥AD ， FN∥DC ， 则∠B =（　　）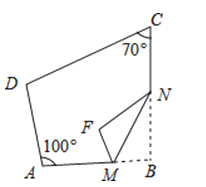

    A.95°
    B.90°
    C.135°
    D.120°

    【答案】A
    【解析】解：∵MF∥AD，FN∥DC，
    ∴∠BMF=∠A=100°，∠BNF=∠C=70°，
    ∵△BMN沿MN翻折得△FMN，
    ∴∠BMN=∠BMF=×100°=50°，
    ∠BNM=∠BNF=×70°=35°，
    在△BMN中，∠B=180°﹣∠BMN﹣∠BNM=180°﹣50°﹣35°=95°．
    故选A．
    【考点精析】认真审题，首先需要了解翻折变换（折叠问题）(折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】以下四组木棒中，哪一组的三条能够刚好做成直角三角形的木架（ ）

    A. 7 cm，12 cm，15 cm B. 7 cm，12 cm，13 cm

    C. 8 cm，15 cm，16 cm D. 3 cm，4 cm，5 cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】单项式﹣3xny2是5次单项式，则n= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】钓鱼岛是中国的固有领土，其渔业资源十分丰富，年捕鱼量达15万吨．数据15万用科学记数法表示为（ ）

    A. 1.5×104B. 15×104C. 1.5×105D. 15×105

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面说法正确的是个数有（ ）

    ①如果三角形三个内角的比是1：2：3，那么这个三角形是直角三角形；

    ②如果三角形的一个外角等于与它相邻的一个内角，则这么三角形是直角三角形；

    ③如果一个三角形的三条高的交点恰好是三角形的一个顶点，那么这个三角形是直角三角形；

    ④如果∠A=∠B=∠C，那么△ABC是直角三角形；

    ⑤若三角形的一个内角等于另两个内角之差，那么这个三角形是直角三角形；

    ⑥在△ABC中，若∠A+∠B=∠C，则此三角形是直角三角形．

    A．3个 B．4个 C．5个 D．6个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】要把一根木条在墙上钉牢，至少需要枚钉子．其中的道理是

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若3是关于x的方程x2﹣x+c=0的一个根，则方程的另一个根等于 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题中，真命题是（ ）

    A.矩形的对角线互相垂直B.菱形的对角线相等

    C.正方形的对角线互相垂直平分且相等D.平行四边形的对角线平分一组对角

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】探究与发现：
    探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？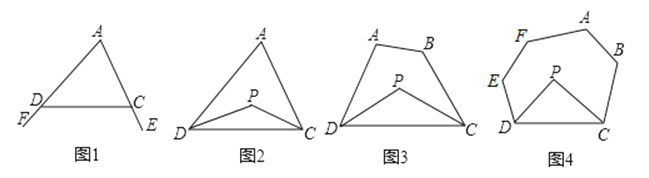

    已知：如图1，∠FDC与∠ECD分别为△ADC的两个外角，试探究∠A与∠FDC+∠ECD的数量关系．
    探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？
    已知：如图2，在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系．
    探究三：若将△ADC改为任意四边形ABCD呢？
    已知：如图3，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系．
    探究四：若将上题中的四边形ABCD改为六边形ABCDEF（图4）呢？
    请直接写出∠P与∠A+∠B+∠E+∠F的数量关系

    查看答案和解析>>

    同步练习册答案