
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?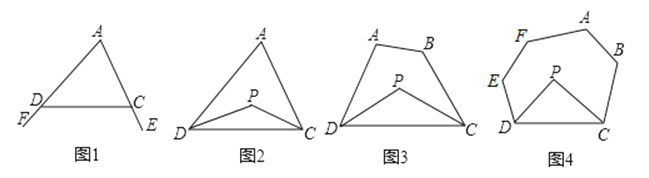
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系
【答案】解:探究一:∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A;
探究二:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠ACD,
∠ACD,
=180°﹣![]() (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°﹣![]() (180°﹣∠A),
(180°﹣∠A),
=90°+![]() ∠A;
∠A;
探究三:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠BCD,
∠BCD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠BCD,
∠BCD,
=180°﹣![]() (∠ADC+∠BCD),
(∠ADC+∠BCD),
=180°﹣![]() (360°﹣∠A﹣∠B),
(360°﹣∠A﹣∠B),
=![]() (∠A+∠B);
(∠A+∠B);
探究四:六边形ABCDEF的内角和为:(6﹣2)180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠P=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠P=180°﹣∠PDC﹣∠PCD,
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠ACD,
∠ACD,
=180°﹣![]() (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°﹣![]() (720°﹣∠A﹣∠B﹣∠E﹣∠F),
(720°﹣∠A﹣∠B﹣∠E﹣∠F),
=![]() (∠A+∠B+∠E+∠F)﹣180°,
(∠A+∠B+∠E+∠F)﹣180°,
即∠P=![]() (∠A+∠B+∠E+∠F)﹣180°.
(∠A+∠B+∠E+∠F)﹣180°.
【解析】探究一:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,再根据三角形内角和定理整理即可得解;
探究二:根据角平分线的定义可得∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,然后根据三角形内角和定理列式整理即可得解;
∠ACD,然后根据三角形内角和定理列式整理即可得解;
探究三:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可;
探究四:根据六边形的内角和公式表示出∠ADC+∠BCD,然后同理探究二解答即可


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,点M , N分别在AB , BC上,将△BMN沿MN翻折,得△FMN , 若MF∥AD , FN∥DC , 则∠B =( )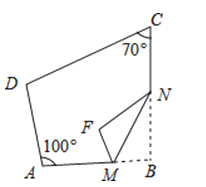
A.95°
B.90°
C.135°
D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查,比较适用普查而不适用抽样调查方式的是( ).
A.调查全省市场上的“N95口罩”是否符合国家标准;
B.调查一批灯泡的使用寿命;
C.调查你所在班级全体学生的身高;
D.调查我市初中生每人每周的零花钱数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB∥CD,E、F分别是AB和CD上的点,DE、AF分别交BC于点G、H,∠A=∠D,试说明:
(1)AF∥ED;
(2)∠1=∠2.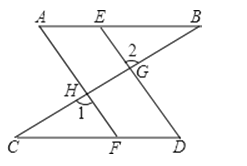
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A.(a﹣b)2=a2﹣b2B.(2a+1)(2a﹣1)=4a﹣1C.(﹣2a3)2=4a6 D.x2﹣8x+16=(x+4)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是两块完全一样的含30°角的直角三角尺,分别记做△ABC与△A′B′C′,现将两块三角尺重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角尺ABC,使其直角顶点C恰好落在三角尺A′B′C′的斜边A′B′上.当∠A=30°,AC=10时,两直角顶点C,C′间的距离是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按如图所示的方式作正方形和等腰直角三角形.若第一个正方形的边长AB=1,第一个正方形与第一个等腰直角三角形的面积和为S1,第二个正方形与第二个等腰直角三角形的面积和为S2……则第n个正方形与第n个等腰直角三角形的面积和Sn=____.
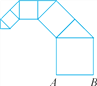
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com