
【题目】如图,已知:AB∥CD,E、F分别是AB和CD上的点,DE、AF分别交BC于点G、H,∠A=∠D,试说明:
(1)AF∥ED;
(2)∠1=∠2.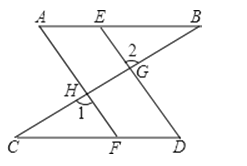
【答案】证明(1):∵AB∥CD,
∴∠A=∠AFC,
∵∠A=∠D,
∴∠AFC=∠D,
∴AF∥ED;
(2)证明:∵AF∥ED,
∴∠1=∠CGD,
又∵∠2=∠CGD,
∴∠1=∠2.
【解析】(1)要证明AF∥ED,根据平行线的判定,只要找到可以判定AF∥ED的条件即可,由题意可以得到,同位角∠AFC=∠D,本题得以解决;
(2)根据第一问的结论AF∥ED,以及对顶角相等,可以证明结论成立.
【考点精析】根据题目的已知条件,利用平行线的判定与性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


科目:初中数学 来源: 题型:
【题目】下面说法正确的是个数有( )
①如果三角形三个内角的比是1:2:3,那么这个三角形是直角三角形;
②如果三角形的一个外角等于与它相邻的一个内角,则这么三角形是直角三角形;
③如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是直角三角形;
④如果∠A=∠B=![]() ∠C,那么△ABC是直角三角形;
∠C,那么△ABC是直角三角形;
⑤若三角形的一个内角等于另两个内角之差,那么这个三角形是直角三角形;
⑥在△ABC中,若∠A+∠B=∠C,则此三角形是直角三角形.
A.3个 B.4个 C.5个 D.6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.在农村电网改造中,四个自然村分别位于如图所示的A,B,C,D处,现计划安装一台变压器,使到四个自然村的输电线路的总长最短,那么这个变压器应安装在AC,BD的交点E处,你知道这是为什么吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?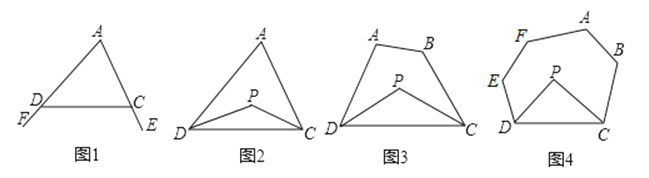
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我校初三年级所有同学的数学成绩,从中抽出500名同学的数学成绩进行调查,抽出的500名考生的数学成绩是( )
A. 总体 B. 样本 C. 个体 D. 样本容量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘轮船在A,B两个码头之间航行,顺水航行需3h,逆水航行需5h.已知水流速度为4km/h,求轮船在静水中的航行速度.若设轮船在静水中的航行速度为xkm/h,则可列式为( )
A. 3x+4=5x﹣4 B. 3(4+x)=5(4﹣x)
C. 3(x+4)=5(x﹣4) D. 3(x﹣4)=5(x+4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com