
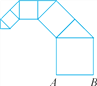
【题目】按如图所示的方式作正方形和等腰直角三角形.若第一个正方形的边长AB=1,第一个正方形与第一个等腰直角三角形的面积和为S1,第二个正方形与第二个等腰直角三角形的面积和为S2……则第n个正方形与第n个等腰直角三角形的面积和Sn=____.
科目:初中数学 来源: 题型:
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?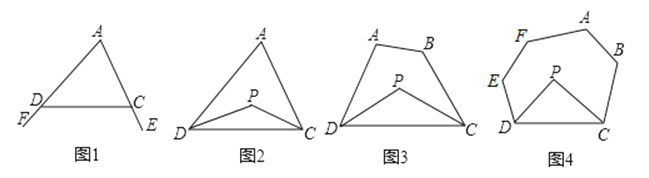
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1 , B1 , C1 , 使A1B=AB,B1C=BC,C1A=CA,顺次连接A1 , B1 , C1 , 得到△A1B1C1 . 第二次操作:分别延长A1B1 , B1C1 , C1A1至点A2 , B2 , C2 , 使A2B1=A1B1 , B2C1=B1C1 , C2A1=C1A1 , 顺次连接A2 , B2 , C2 , 得到△A2B2C2 , …按此规律,要使得到的三角形的面积超过2010,最少经过( )次操作.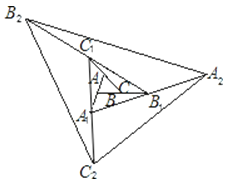
A.6
B.5
C.4
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]()
(2)(p﹣q)4÷(q﹣p)3(p﹣q)2
(3)aa2a3+(﹣2a3)2﹣a8÷a2
(4)(﹣2x)2(x2)3÷(﹣x)2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘轮船在A,B两个码头之间航行,顺水航行需3h,逆水航行需5h.已知水流速度为4km/h,求轮船在静水中的航行速度.若设轮船在静水中的航行速度为xkm/h,则可列式为( )
A. 3x+4=5x﹣4 B. 3(4+x)=5(4﹣x)
C. 3(x+4)=5(x﹣4) D. 3(x﹣4)=5(x+4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市平均每天产生垃圾700 t,由甲、乙两家垃圾处理厂处理.已知甲厂每小时可处理垃圾55 t,费用为550元;乙厂每小时可处理垃圾45 t,费用为495元.
(1)如果甲、乙两厂同时处理该城市的垃圾,那么每天需几小时?
(2)如果该城市规定每天用于处理垃圾的费用不得高于7370元,那么至少安排甲厂处理几小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医院为支援武汉,经自愿申请遴选了5名医护人员组成“志愿小分队”,5名医护人员的年龄分别为(单位:岁)24,25,24,27,32.则这组数据的中位数和众数分别是( )
A.24岁和24岁B.25岁和24岁C.25岁和27岁D.26岁和27岁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com