练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．计算：（8a+$\frac{2}{a}$-8）÷（$\sqrt{\frac{1}{2a}}$-$\sqrt{2a}$）（0＜a＜$\frac{1}{2}$）

    分析 首先化简二次根式，进而利用因式分解法化简分式求出即可．

    解答 解：（8a+$\frac{2}{a}$-8）÷（$\sqrt{\frac{1}{2a}}$-$\sqrt{2a}$）
    =$\frac{8{a}^{2}-8a+2}{a}$÷（$\frac{\sqrt{2a}}{2a}$-$\sqrt{2a}$）
    =$\frac{2（2a-1）^{2}}{a}$×$\frac{2a}{（1-2a）\sqrt{2a}}$
    =$\frac{2（1-2a）\sqrt{2a}}{a}$．

    点评 此题主要考查了二次根式的混合运算，正确化简二次根式是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．如图，有一块20米，宽为8米的矩形空地，计划在其中修建两条人行通道（黑色区域），剩余绿地面积之和为126米2，若纵向的人行横道的宽是横向的人行通道的宽的2倍．
    （1）问横向的人行横道的宽度是多少米？
    （2）这一矩形绿化工程由1人，三个星期完成，第一个星期工人只绿化6米2，若想三个星期全部绿化完毕，那么这个星期的平均增长的绿化率为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，在△ABC中，∠ACB=90°，点D在边AB上，DB=DC，说明△ACD为等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

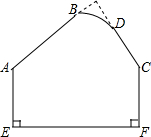    6．如图所示的模板，规定：AB、CD的延长线应相交成80°的角，因交点不在模板上，不便测量，工人师傅测得∠BAE=124°，∠DCF=155°，此时AB，CD的延长线相交所成的角是否符合规定？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．设平行四边形ABCD的顶点A（-2，1），一组对边AB、CD的中点分别为M（3，0），N（-1，2），求其它点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知a、b是一个等腰三角形的两边长，且满足a2+b2-4a-6b+13=0，求这个等腰三角形的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

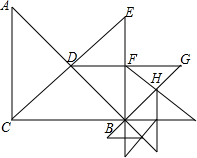    10．如图，在Rt△ABC中，∠ACB=90°，AC=BC=$\sqrt{2}$，CD⊥AB，垂足为D，以BD为一条直角边向三角形外作第二个等腰Rt△BDE，再以BF为一条直角边向三角形外作第三个等腰Rt△BFG，如此下去，如果Rt△ABC的斜边为记为c1，论上述方法所作的等腰直角三角形的斜边依次记为c2、c3、c4、…、cn，则c2015=$\frac{（\sqrt{2}）^{2014}}{{2}^{2013}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

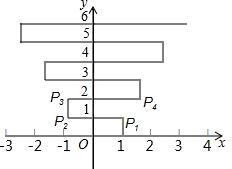    7．如图，在平面直角坐标系上有个点P（1，0），点P第1次向上跳动1个单位至点P1（1，1），紧接着第2次向左跳动2个单位至点P2（-1，1），第3次向上跳动1个单位，第4次向右跳动3个单位，第5次又向上跳动1个单位，第6次向左跳动4个单位，…，依此规律跳动下去，点P第100次跳动至点P100的坐标是（　　）
    A．（100，50）B．（50，50）C．（25，50）D．（26，50）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．一次函数y=ax+5a（a≠0）与二次函数y=x2+2x-b（b≠0）交于x轴上一点，则当-2≤x≤3时二次函数y=x2+2x-b（b≠0）的最小值为-16．

    查看答案和解析>>

    同步练习册答案