
 如图,在平面直角系中点A(1,3),点 B(3,1),点P、Q分别在x轴、y轴上运动,求四边形PBAQ的最小值.
如图,在平面直角系中点A(1,3),点 B(3,1),点P、Q分别在x轴、y轴上运动,求四边形PBAQ的最小值. 分析 作A点关于y轴的对称点C,B点关于x轴的对称点D,根据对称的性质得到C点坐标为(-1,3),D点坐标为(3,-1),CD分别交x轴、y轴于P点、Q点,根据两点之间线段最短得此时四边形PBAQ的周长最小.根据两点间的距离公式求出即可.
解答 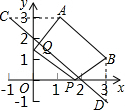 解:作A点关于y轴的对称点C,B点关于x轴的对称点D,所以C点坐标为(-1,3),D点坐标为(3,-1),
解:作A点关于y轴的对称点C,B点关于x轴的对称点D,所以C点坐标为(-1,3),D点坐标为(3,-1),
连结CD分别交x轴、y轴于P点、Q点,此时四边形PBAQ的周长最小,
∴四边形PBAQ的周长最小值=CD,
∵CD=$\sqrt{(-1-3)^{2}+(3+1)^{2}}$=4$\sqrt{2}$,
AB=$\sqrt{(1-3)^{2}+(3-1)^{2}}$=2$\sqrt{2}$,
∴四边形PBAQ的最小值=4$\sqrt{2}$+2$\sqrt{2}$=6$\sqrt{2}$.
点评 此题主要考查了轴对称-最短路线问题,以及两点间的距离公式,得出P点,Q点的位置是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 34.5% | B. | 33% | C. | 30% | D. | 27% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠A=∠C-∠B | B. | ∠A:∠B:∠C=1:2:3 | C. | a2=(b+c)(b-c) | D. | a=1,b=2,c=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
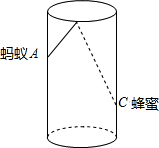 如图,圆柱形玻璃杯,高为8cm,底面周长为12cm,在杯内离杯底2cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,求蚂蚁到达蜂蜜的最短距离.
如图,圆柱形玻璃杯,高为8cm,底面周长为12cm,在杯内离杯底2cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,求蚂蚁到达蜂蜜的最短距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com