
����Ŀ��ij��ѧ������1�����40��ͬѧ����һ��30���������������ǵijɼ�ͳ�����±���
������/�� | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
�� �� | 1 | 2 | 8 | 11 | 5 |
����Щ���ݰ����5���������飬���Ƴ���ͼ��Ƶ���ֲ�ֱ��ͼ������������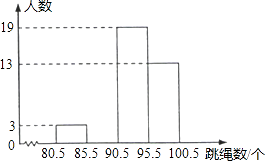
��1�������п�ȱ��������д����������ȫƵ���ֲ�ֱ��ͼ��
��2�������ͬѧ��������ɼ���������������λ��������
��3��������90���ɵ����֣�ѧУ�����꼶����720�ˣ��Թ��Ƹ���ѧ�����꼶���ж������������ܵ����֣�
���𰸡�
��1���⣺����ֱ��ͼ�õ�95.5��100.5С�鹲��13�ˣ���ͳ�Ʊ�֪����100������5�ˣ�
����98������13��5=8�ˣ�
��90������40��1��2��8��11��8��5=5�ˣ�
��ͳ�Ʊ�Ϊ��
������/�� | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
�� �� | 1 | 2 | 5 | 8 | 11 | 8 | 5 |
ֱ��ͼΪ��
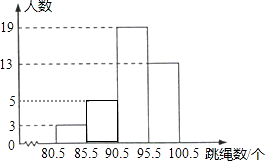
��2��95,95
��3���⣺���Ƹ���ѧ�����꼶���ܵ����ֵ���720�� ![]() =54��
=54��
���������⣺��2���۲�ͳ�Ʊ�֪������Ϊ95������λ��Ϊ95����
��2������ �dz��ִ����������ݣ���λ���뽫���ݴ�С�������У��������м��һ���������м����������ƽ��������3����������������������ԣ����Թ�������Լ��720�� 0.075=54��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺С���Ȱ���ѧ���ڿ������Ͽ�����һ����Ȥ�Ķ������������߳������������������ߵ�ƽ���͵��ڵ����ߵ�һ����������ϵ����ߵ�ƽ���͵���������ͼ1���ڡ�ABC�У���DΪBC���е㣬���ݡ����߳����������ɵã�
AB2+AC2=2AD2+2BD2 �� С�����Զ�������֤�������ֹ������£�
�⣺����A��AE��BC�ڵ�E����ͼ2����Rt��ABE�У�AB2=AE2+BE2 ��
ͬ���ɵã�AC2=AE2+CE2 �� AD2=AE2+DE2 ��
Ϊ֤���ķ��㣬������BD=CD=x��DE=y��
��AB2+AC2=AE2+BE2+AE2+CE2=��
��1���������С��ʣ���֤�����̣�
�������ã�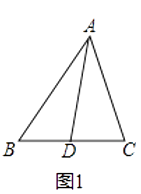
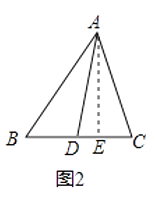
��2�����ڡ�ABC�У���DΪBC���е㣬AB=6��AC=4��BC=8����AD=��
����ͼ3����O�İ뾶Ϊ6����A��Բ�ڣ���OA=2 ![]() ����B�͵�C�ڡ�O�ϣ��ҡ�BAC=90�㣬��E��F�ֱ�ΪAO��BC���е㣬��EF�ij�Ϊ
����B�͵�C�ڡ�O�ϣ��ҡ�BAC=90�㣬��E��F�ֱ�ΪAO��BC���е㣬��EF�ij�Ϊ
��չ���죺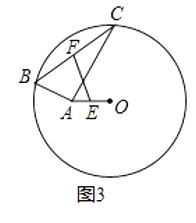
��3��С�����������������뵽������ѵ�����ϵ���Ŀ����ͼ4����֪��O�İ뾶Ϊ5 ![]() ����A����3��4��Ϊֱ�Ƕ���ġ�ABC������������B��C���ڡ�O�ϣ�DΪBC���е㣬��AD�������ֵ��
����A����3��4��Ϊֱ�Ƕ���ġ�ABC������������B��C���ڡ�O�ϣ�DΪBC���е㣬��AD�������ֵ��
������������ķ����ͽ��ۣ����AD�������ֵ��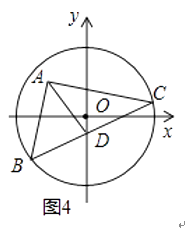
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��![]() ֱ��
ֱ��![]() �ֱ�
�ֱ�![]() �ڵ�
�ڵ�![]() ��
��![]() �Ľ�ƽ���߽��ڵ�
�Ľ�ƽ���߽��ڵ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ��
��![]() ��
��

��1����֤��![]()
��2����ͼ2������![]() Ϊ
Ϊ![]() ��һ���㣬
��һ���㣬![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() �Ĵ�С�Ƿ����仯�������䣬�����ֵ�����ı䣬��˵�����ɣ�
�Ĵ�С�Ƿ����仯�������䣬�����ֵ�����ı䣬��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B�������50km������ij�������г���A�س���ʻ��B�أ���Ҳ��ͬ��������Ħ�г���A�س���ʻ��B�أ�������仯�����У���������ʻ��·���ñ���s��km����ʾ�������õ�ʱ���ñ���t��ʱ����ʾ��ͼ������OPQ���߶�MN�ֱ��ʾ��������ʻ��·��s��ʱ��t�ı仯��ϵ�������ͼ��ش�

��1��ֱ��д�����׳�����______Сʱ���Ҳſ�ʼ������
��2����ֱ�����׳���1Сʱ����ٶȺ��ҵ���ʻ�ٶȣ�
��3��������ʻ��Сʱ���ϼף���ʱ���˾�B�ػ��ж���ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCDΪ���Σ�H��F�ֱ�ΪAD��BC�ߵ��е㣬�ı���EFGHΪ���Σ�E��G�ֱ���AB��CD���ϣ���ͼ���ĸ�ֱ�����������֮�������EFGH�����֮��Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����߲�Ʒ�ĸ���ֵ��ij��˾�ƻ����з�������1200���²�Ʒ���о��ӹ�����Ͷ���г������мס��������������߱��ӹ���������˾�ɳ������Ա�ֱ������乤���˽���������������Ϣ��
��Ϣһ�����������ӹ����������Ʒ���ҹ��������ӹ����������Ʒ����10�죻
��Ϣ�����ҹ���ÿ��ӹ��������Ǽ���ÿ��ӹ�������1.5����
����������Ϣ����ס�����������ÿ��ֱ��ܼӹ����ټ��²�Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����MON=90������A��B�ֱ���OM��ON���˶��������O�غϣ���
��1����ͼ�٣�AE��BE�ֱ��ǡ�BAO�͡�ABO��ƽ���ߣ����ŵ�A����B���˶�����AEB=������
��2����ͼ�ڣ���BC�ǡ�ABN��ƽ���ߣ�BC�ķ����ӳ������OAB��ƽ���߽��ڵ�D
������BAO=60�������D=������������
�����ŵ�A��B���˶�����D�Ĵ�С�����������ᣬ���D�Ķ���������ᣬ��˵�����ɣ�
��3����ͼ�ۣ��ӳ�MO��Q���ӳ�BA��G����֪��BAO����OAG��ƽ�������BOQ��ƽ�������ӳ����ཻ�ڵ�E��F������![]() �У������һ��������һ���ǵ�3�������ABO�Ķ�����
�У������һ��������һ���ǵ�3�������ABO�Ķ�����



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AC=BD��E��F��G��H�ֱ���AB��BC��CD��DA���е㣬��EG��FH���ڵ�O����AC=4����EG2+FH2=______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼAB�ǡ�O��ֱ������CΪ��O��һ�㣬AE����C�������ഹֱ������ΪE��AE����O�ڵ�D��ֱ��EC��AB���ӳ����ڵ�P������AC��BC��PC=2PB��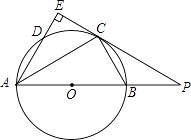
��1��̽���߶�PB��AB֮���������ϵ����˵�����ɣ�
��2����AD=3����AB����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com