

���� ��1����֤����ABQ�ա�CAP���Ӷ��õ���BAQ=��ACP��Ȼ�����������ε���ǵ�������⼴�ɣ�
��2����֤����ACQ�ա�CBP���Ӷ��õ���CAQ=��BCPȻ�����ݡ�CAM+��ACM=��BCP+��ACM��⼴�ɣ�
��� �⣺��1����CMQ=60�㲻�䣮
�ߡ�ABCΪ�ȱ������Σ�
��CA=AB����CAP=��ABQ=60�㣮
��AP=BQ��
���CAP�ա�ABQ��
���ACP=��BAQ��
���CMQ=��ACM+��MAC=��BAQ+��MAC=60�㣮
��2����CMQ=120�㲻��
�ߡ�ABCΪ�ȱ������Σ�
��CA=AB=BC����ACB=��ABC=60�㣮
���ACQ=��CBP=120�㣮
��AP=BQ��
��CQ=BP��
���ACQ�ա�CBP��
���CAQ=��BCP��
���CMQ=��CAM+��ACM=��BCP+��ACM=180��-60��=120�㣮
���� ���⿼��ȱ������ε����ʡ�ȫ�������ε��ж������ʣ����յȱ������ε����ʡ�ȫ�������ε��ж��������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�PM��QN�ֱ���AB��AC�Ĵ�ֱƽ���ߣ���BAC=110�㣬BC=18�����PAQ=40�㣬���APQ���ܳ�Ϊ18��
��ͼ���ڡ�ABC�У�PM��QN�ֱ���AB��AC�Ĵ�ֱƽ���ߣ���BAC=110�㣬BC=18�����PAQ=40�㣬���APQ���ܳ�Ϊ18���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
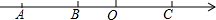 ��ֵ����ͼ��ʵ��a��b��c�������ϵĶ�Ӧ��ֱ�ΪA��B��C��OΪԭ�㣩����$\sqrt{��a+b��^{2}}$-|c-b|-|a+c|��ֵ��
��ֵ����ͼ��ʵ��a��b��c�������ϵĶ�Ӧ��ֱ�ΪA��B��C��OΪԭ�㣩����$\sqrt{��a+b��^{2}}$-|c-b|-|a+c|��ֵ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com