
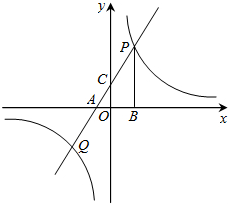
 如图,经过点A(-2,0)的一次函数y=ax+b(a≠0)与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB=$\frac{3}{2}$,点B的坐标为(4,0).
如图,经过点A(-2,0)的一次函数y=ax+b(a≠0)与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB=$\frac{3}{2}$,点B的坐标为(4,0).分析 (1)利用tan∠PAB=$\frac{3}{2}$,以及点B坐标为(4,0),点A(-2,0),即可得出AB的长,进而得出P点坐标,分别代入函数解析式求出即可;
(2)利用两函数解析式得出交点坐标,即可得出对应线段之间的关系,即可得出△PQB的面积.
解答 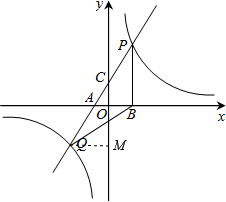 解:(1)∵BO=4,AO=2,
解:(1)∵BO=4,AO=2,
∴AB=6,
∵tan∠PAB=$\frac{PB}{AB}$=$\frac{3}{2}$,
∴PB=9,
∴P点坐标为:(4,9),
把P(4,9),代入反比例函数解析式y=$\frac{k}{x}$,得k=36,
∴反比例函数解析式为y=$\frac{36}{x}$;
把点A(-2,0),P(4,9),代入y=ax+b得:$\left\{\begin{array}{l}{-2a+b=0}\\{4a+b=9\\;}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=3}\end{array}\right.$,
故一次函数解析式为y=$\frac{3}{2}$x+3.
(2)过点Q作QM⊥y轴于点M,
由 $\left\{\begin{array}{l}{y=\frac{3}{2}x+3}\\{y=\frac{36}{x}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=9}\end{array}\right.$或$\left\{\begin{array}{l}{x=-6}\\{y=-6}\end{array}\right.$,
∴Q点坐标为:(-6,-6),
∴S△PQB=$\frac{1}{2}$•PB•QM
=$\frac{1}{2}$×9×(6+4)
=45.
点评 此题主要考查了待定系数法求一次函数与反比例函数解析式,根据图形得出三角形底与高的长度是解决问题的关键.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.05×102 | B. | 1.05×104 | C. | 1.05×105 | D. | 1.05×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
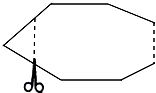 如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的对角线条数为( )
如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的对角线条数为( )| A. | 77 | B. | 90 | C. | 65 | D. | 104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2011}$ | B. | $\sqrt{2012}$ | C. | $\sqrt{2013}$ | D. | $\sqrt{2014}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{28}$ | B. | $\sqrt{43}$ | C. | $\sqrt{58}$ | D. | $\root{3}{39}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com