
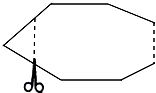
 如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的对角线条数为( )
如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的对角线条数为( )| A. | 77 | B. | 90 | C. | 65 | D. | 104 |
分析 根据多边形内角和公式,可得新多边形的边数,根据新多边形比原多边形多1条边可得多边形的边数,再计算出对角线的条数.
解答 解:设新多边形是n边形,由多边形内角和公式得
(n-2)180°=2340°,
解得n=15,
15-1=14,
$\frac{1}{2}$×14×(14-3)=77.
故原多边形的对角线条数为77.
故选:A.
点评 本题考查了多边形内角与外角,多边形的内角和公式是解题关键.同时考查了多边形的对角线,n边形从一个顶点出发可引出(n-3)条对角线.从n个顶点出发引出(n-3)条,而每条重复一次,所以n边形对角线的总条数为:$\frac{1}{2}$n(n-3)(n≥3,且n为整数)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 已知平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,2),B(1,-1),C(3,0).画出以点O为位似中心,放大△ABC到原来的2倍的△A′B′C′.
已知平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,2),B(1,-1),C(3,0).画出以点O为位似中心,放大△ABC到原来的2倍的△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩(单位:米) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 | 1.85 | 1.90 |
| 人数 | 2 | 3 | 2 | 4 | 5 | 2 | 1 | 1 |
| A. | 这些运动员成绩的中位数是1.70 | B. | 这些运动员成绩的众数是5 | ||
| C. | 这些运动员的平均成绩是1.71875 | D. | 这些运动员成绩的方差是0.0725 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不论k为何值,图象一定经过(1,0)和(-1,0) | |
| B. | 不论k为何值,函数一定有最大值或最小值 | |
| C. | 当x≤1时 y随x的增大而增大,则k的取值范围是k≤3 | |
| D. | 不论k为何值,图象与x轴一定有公共点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
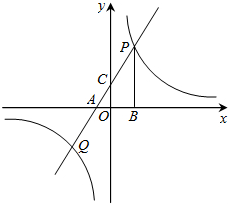 如图,经过点A(-2,0)的一次函数y=ax+b(a≠0)与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB=$\frac{3}{2}$,点B的坐标为(4,0).
如图,经过点A(-2,0)的一次函数y=ax+b(a≠0)与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB=$\frac{3}{2}$,点B的坐标为(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1.5 | B. | $-\frac{2}{3}$ | C. | 1.5 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com