
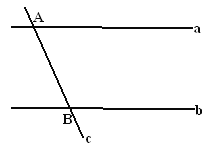
【题目】如图,a、b、c是三条公路,且a∥b,加油站M到三条公路的距离相等.(1)确定加油站M的位置.(保留作图痕迹,不写作法)
(2)一辆汽车沿公路c由A驶向B,行使到AB中点时,司机发现油料不足,仅剩15升汽油,需要到加油站加油,已知从AB中点有路可直通加油站,若AB相距200千米,汽车每行使100千米耗油12升,请判断这辆汽车能否顺利到达加油站?为什么?
【答案】(1)见解析;(2)这辆汽车能顺利到达加油站.
【解析】
(1)到两条相交公路距离相等的点在这两条公路所在的直线的夹角的平分线上,那么点M是三条直线所夹角的角平分线的交点,位于AB的右侧;
(2)由角平分线易得∠AMB是直角三角形,那么斜边中点到加油站的距离等于斜边的一半,求得到加油站的距离,得到的相应的耗油量,和100千米的耗油量比较即可.
(1)如图所示,即点M为所求;
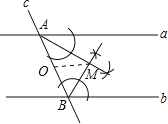
(2)能.由作图可知AM、BM分别是角平分线,又a∥b,
∴△ABM是直角三角形,0是中点,
∴![]() ,
,
又AB=200千米,
∴OM=100千米,
汽车每行使100千米耗油12升,12<15,
∴这辆汽车能顺利到达加油站.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
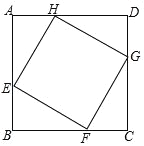
【题目】如图,正方形ABCD的边长为8,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH.
(1)判断四边形EFGH的形状.(直接写结论,不必证明)
(2)设BE=x,四边形EFGH的面积为S,请真接写出S与x的数解析式,并求出S的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°, AD是∠BAC的平分线,O是AB上一点, 以OA为半径的⊙O经过点D.

(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,∠D=90°,BC=CD=12,∠ABE=45°,点E在DC上,AE,BC的延长线相交于点F,若AE=10,则S△ADE+S△CEF的值是______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
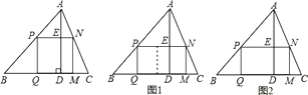
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公园里有甲、乙两组游客正在做团体游戏,两组游客的年龄如下:(单位:岁)
甲组:13,13,14,15,15,15,15,16,17,17;
乙组:3,4,4,5,5,6,6,6,54,57.
我们很想了解一下甲、乙两组游客的年龄特征,请你运用“数据的代表”的有关知识对甲、乙两组数据进行分析,帮我们解决这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴、y轴的正半轴上,且OA=4,OC=3,若抛物线经过O,A两点,且顶点在BC边上,点E的坐标分别为(0,1),对称轴交BE于点F.
(1)求该抛物线的表达式;
(2)点M在对称轴右侧的抛物线上,点N在x轴上,请问是否存在以点A,F,M,N为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
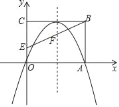
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家销售一款商品,进价每件80元,售价每件145元,每天销售40件,每销售一件需支付给商场管理费5元,未来一个月![]() 按30天计算
按30天计算![]() ,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天
,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天![]() 且x为整数
且x为整数![]() 的销售量为y件.
的销售量为y件.
![]() 直接写出y与x的函数关系式;
直接写出y与x的函数关系式;
![]() 设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com