Question

阅读理解
（1）发现一：
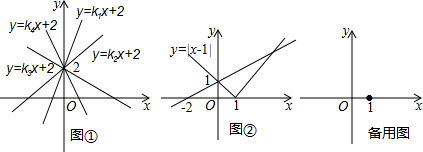
一次函数y=kx+b（k、b为常数且k≠0），若k的绝对值越大，此一次函数的图象与过点（0，b）且平行于x轴的直线所夹的锐角就越大．
根据发现请解决下列问题：图①是y=k₁x+2、y=k₂x+2、y=k₃x+2、y=k₄x+2四个一次函数在同一坐标系中的图象，比较k₁、k₂、k₃、k₄的大小

 

．（用“＜”或“＞”号连接）
（2）发现二：
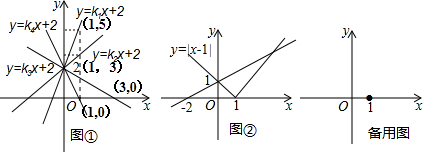
我们知道函数y₁=k₁x+b₁与y₂=k₂x+b₂的交点的横坐标是方程k₁x+b₁=k₂x+b₂的解．类似的，|x-1|=

1

2

x+1的解就是y=|x-1|和y=

1

2

x+1的两个图象交点的横坐标．
求含有绝对值的方程|x-1|=

1

2

x+1的解．
解：在同一直角坐标系中画出y=|x-1|，y=

1

2

x+1的图象如图②．
由图象可知方程|x-1|=

1

2

x+1的解有两个．
情况一：由图象可知当x＞1时，y=|x-1|=x-1，即x-1=

1

2

x+1，解得x=4
情况二：由图象可知当x≤1时，y=|x-1|=-x+1，即-x+1=

1

2

x+1，解得x=0
所以方程|x-1|=

1

2

x+1的解为x₁=4、x₂=0
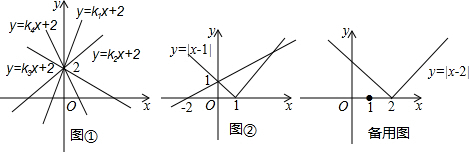
利用以上方法，解关于x的方程|x-2|=-

1

2

x+1．
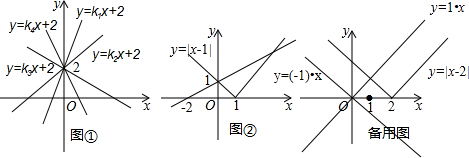
（3）拓展延伸
解关于x的方程|x-2|=ax（a为常数且a≠0）．（用含a的代数式表示）

Answer 1

考点：一次函数综合题

专题：

分析：（1）想知道k之间的大小关系，图中又无其他信息，对此我们可以自己找点来近似的估计k值，如可近似估计四条线上的各一个异于（0，2）的点，然后代入求出k₁、k₂、k₃、k₄．再比较即可．
（2）仿照例题，有图象看出交点情况，每个交点都表示方程有一个解，其解即为其横坐标，这是函数的性质．
（3）在坐标系中画出y=|x-2|图象，则其与y=ax图象的交点情况即表示方程|x-2|=ax的解的情况．因为对y=ax，当x=0时，y=0，所以直线y=ax必过原点O，即图象可能为任一过点O的直线以点O为中心旋转360°过程中的任一情况，考虑全面，再利用（1）的性质、（2）的方法求解即可．此处可以做y=（-1）•x和y=1•x的图象作为考虑问题的参考．

解答：解：
（1）k₄＜k₃＜k₂＜k₁．
下为分析过程，不用作答．

如图近似估计四条线上的各一个异于（0，2）的点，然后代入求出k₁、k₂、k₃、k₄．再比较即可．

（2）如图，在坐标系中画出y=|x+2|和y=-

1

2

x+1的图象，
由图象可知方程|x+2|=

1

2

 x+1的解有两个．
情况一：当x＞-2时，y=|x+2|=x+2，即x+2=-

1

2

x+1，解得x=-

2

3

．
情况二：当x≤-2时，y=|x+2|=-x-2，即-x-2=-

1

2

x+1，解得x=-6．
∴方程|x+2|=-

1

2

x+1的解为x₁=-

2

3

或 x₂=-6．
（3）

如图，在坐标系中画出y=|x-2|图象，则其与y=ax图象的交点情况即表示方程|x-2|=ax的解的情况．
∵对y=ax，当x=0时，y=0，
∴直线y=ax必过原点O，即图象可能为任一过点O的直线以点O为中心旋转360°过程中的任一情况，
∴图象分为过一、三象限，过二、四象限，与x轴重合，与y轴重合四种情况．
由（1）知，直线过一、三象限时，a＞0，a越大，锐角越大；过二、四象限时，a＜0，a越小，锐角越大；与x轴重合，a=0，与y轴重合，a不存在．且对y=kx+b，k相等的直线平行．
如图，画y=（-1）•x和y=1•x的图象，

观察可知，
当a＜-1时，有一个解，此时x＜2，y=|x-2|=-x+2，即-x+2=ax，解得x=

2

a+1

；
当-1≤a＜0时，无解；
当0＜a＜1时，有两个解，当x＜2时，y=|x-2|=-x+2，即-x+2=ax，解得x=

2

a+1

；当x＞2时，y=|x-2|=x-2，即x-2=ax，解得x=-

2

a-1

；
当a≥1时，有一个解，此时x＜2，y=|x-2|=-x+2，即-x+2=ax，解得x=

2

a+1

．

点评：本题考察学生对直线y=kx+b这个基本解析式的理解，尤其是对其中两个系数k，b的掌握和理解，同时考查学生的学习、理解能力，是否能够够举一反三，总体来说对学生要求比较高．另外题目所展示的性质和方法是数形结合解决方程的重要方法之一，虽然尚未深入学习，但非常值得理解、体会、应用．