
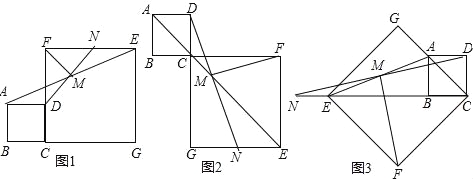
����Ŀ����ͼ1��ʾ����������ABCD��������CGEF�У���B��C��G��ͬһ��ֱ���ϣ�M���߶�AE���е㣬DM���ӳ��߽�EF�ڵ�N������FM����֤��DM=FM��DM��FM������д֤�����̣�
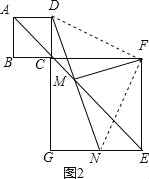
��1����ͼ2������B��C��F��ͬһ��ֱ���ϣ�DM���ӳ��߽�EG�ڵ�N�������������䣬��̽���߶�DM��FM�������Ĺ�ϵ����д�����룬������֤����
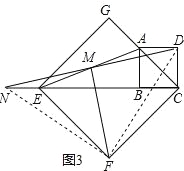
��2����ͼ3������E��B��C��ͬһ��ֱ���ϣ�DM���ӳ��߽�CE���ӳ����ڵ�N�������������䣬̽���߶�DM��FM�������Ĺ�ϵ����ֱ��д�����룮
���𰸡���1��DM��FM��DM=FM��֤����������
��2��DM��FM��DM=FM��
��������
�����������1������DF��NF�����ı���ABCD��CGEF�������Σ��õ�AD��BC��BC��GE�����ǵõ�AD��GE����á�DAM=��NEM��֤�á�MAD�ա�MEN���ó�DM=MN��AD=EN���Ƴ���MAD�ա�MEN��֤����DFN�ǵ���ֱ�������Σ����ɵõ����ۣ�
��2������DF��NF�����ı���ABCD�������Σ��õ�AD��BC���ɵ�E��B��C��ͬһ��ֱ���ϣ����ǵõ�AD��CN����á�DAM=��NEM��֤�á�MAD�ա�MEN���ó�DM=MN��AD=EN���Ƴ���MAD�ա�MEN��֤����DFN�ǵ���ֱ�������Σ����ǽ��۵õ���
�����������1����ͼ2��DM=FM��DM��FM��
֤��������DF��NF��
���ı���ABCD��CGEF�������Σ�
��AD��BC��BC��GE��
��AD��GE��
���DAM=��NEM��
��M��AE���е㣬
��AM=EM��
�ڡ�MAD���MEN�У�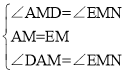 �����MAD�ա�MEN����DM=MN��AD=EN��
�����MAD�ա�MEN����DM=MN��AD=EN��
��AD=CD����CD=NE����CF=EF����DCF=��DCB=90�㣬
�ڡ�DCF���NEF�У�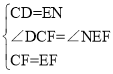 �����MAD�ա�MEN����DF=NF����CFD=��EFN��
�����MAD�ա�MEN����DF=NF����CFD=��EFN��
�ߡ�EFN+��NFC=90�㣬���DFC+��CFN=90�㣬���DFN=90�㣬
��DM��FM��DM=FM
��2�����룺DM��FM��DM=FM��
֤�����£���ͼ3������DF��NF������DF��NF��
���ı���ABCD�������Σ���AD��BC���ߵ�E��B��C��ͬһ��ֱ���ϣ�
��AD��CN�����ADN=��MNE��
�ڡ�MAD���MEN�У�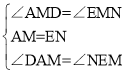 ��
��
���MAD�ա�MEN����DM=MN��AD=EN����AD=CD����CD=NE����CF=EF���ߡ�DCF=90��+45��=135�㣬��NEF=180�㩁45��=135�㣬���DCF=��NEF��
�ڡ�DCF���NEF�У�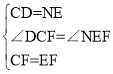 �����MAD�ա�MEN����DF=NF����CFD=��EFN��
�����MAD�ա�MEN����DF=NF����CFD=��EFN��
�ߡ�CFD+��EFD=90�㣬���NFE+��EFD=90�㣬���DFN=90�㣬
��DM��FM��DM=FM��


 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+2x+![]() =0����������ȵ�ʵ������kΪ��������
=0����������ȵ�ʵ������kΪ��������
��1����k��ֵ��
��2�����˷�����һ��Ϊ��ʱ��ֱ��y=x+2�����x�Ķ��κ���y=x2+2x+![]() ��ͼ����A��B���㣬��M���߶�AB�ϵ�һ�����㣬����M��MN��x�ᣬ�����κ�����ͼ���ڵ�N�����߶�MN�����ֵ����ʱ��M�����ꣻ
��ͼ����A��B���㣬��M���߶�AB�ϵ�һ�����㣬����M��MN��x�ᣬ�����κ�����ͼ���ڵ�N�����߶�MN�����ֵ����ʱ��M�����ꣻ
��3������2���еĶ��κ���ͼ��x���·��IJ�����x�ᷭ�۵�x���Ϸ���ͼ������ಿ�ֱ��ֲ��䣬���ۺ��ͼ����ԭͼ��x���Ϸ��IJ������һ����W����״����ͼ����ֱ��y=![]() x+b�����ͼ��ǡ�������������㣬��b��ֵ��
x+b�����ͼ��ǡ�������������㣬��b��ֵ��
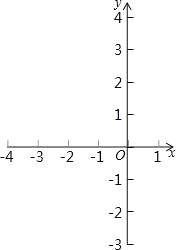
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ֵ�ӰƱÿ��20Ԫ,���ֵ�ӰƱÿ��15Ԫ,������ס������ֵ�ӰƱ��40��,ǡ����ȥ700Ԫ,����ֵ�ӰƱ����____��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ĸ��ǰϦ��ij�Ա������ӳ��ҹ���A��B������У���֪A��B������еĵ��۱�Ϊ2��3�����ۺ�Ϊ200Ԫ��
��1����A��B������еĵ��۷ֱ��Ƕ���Ԫ��
��2���õ����������������ǡ����ȥ9600Ԫ���ҹ���A��������36����B����е�����������A�����������2�������м��ֽ���������
��3�������г����飬����һ��A����пɻ���10Ԫ������һ��B����пɻ���18Ԫ��Ϊ���װ��ģ��õ�������ÿ�۳�һ��B����У�Ϊ���Ĺ��������mԪ��ÿ��A����е����䣬�ڣ�2���������£�Ҫʹ���ȫ���۳������з���������ͬ��mֵ�Ƕ��٣���ʱ������������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ʒ�Ľ���Ϊ80Ԫ�����Ϊ100Ԫ�������ڸ���Ʒ��ѹ���̵����������ۣ�Ҫ��֤�����ʲ�����12.5%��������Ʒ���ɴ� ��
A.����B.����C.����D.����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
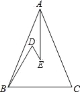
����Ŀ����ͼ������ABC�У�AB=AC��D��E����ABC�ڵ����㣬AEƽ����BAC����D=��DBC=60������BD=5cm��DE=3cm����BC�ij��� cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������Ե�AΪ���ŵ�4�������а������ں����ϵ�B����һ�Һ��ബ������C��ȥִ����������ABC=45�㣬��ACB=37�㣬B��C�������10���������Һ��ബ��BCֱ�Ӻ��У����д�����Σ������˵�����ɣ�
���ο����ݣ�sin37����0.60��cos37����0.80��tan37����0.75��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com