
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНaЃЈx2ЃcxЃ2c2ЃЉЃЈaЃО0ЃЉНЛxжсгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌНЛyжсгкЕуCЃЎ
ЃЈ1ЃЉ ШЁAЃЈЃ1ЃЌ0ЃЉЃЌдђЕуBЕФзјБъЮЊ___________ЃЛ
ЃЈ2ЃЉ ШєAЃЈЃ1ЃЌ0ЃЉЃЌaЃН1ЃЌЕуPЮЊЕквЛЯѓЯоЕФХзЮяЯпЃЌвдPЮЊдВаФЃЌ![]() ЮЊАыОЖЕФдВЧЁКУгыACЯрЧаЃЌЧѓPЕузјБъЃЛ
ЮЊАыОЖЕФдВЧЁКУгыACЯрЧаЃЌЧѓPЕузјБъЃЛ
ЃЈ3ЃЉ ШчЭМЃЌЕуRЃЈ0ЃЌnЃЉдкyжсИКАыжсЩЯЃЌжБЯпRBНЛХзЮяЯпгкСэвЛЕуDЃЌжБЯпRAНЛХзЮяЯпгкEЃЎШєDRЃНDBЃЌEFЁЭyжсгкFЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
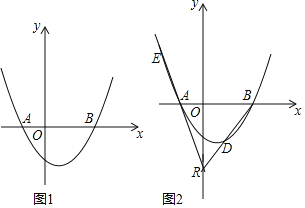
ЁОД№АИЁП(1) B(2ЃЌ0)(2) P(3ЃЌ4)(3) ![]()
ЁОНтЮіЁПЃЈ1ЃЉНЋAЕФзјБъДњШыЃЌЧѓГіcМДПЩЕУГіЕуBЕФзјБъЃЌАбaЃЌcДњШыЕуCЕФзјБъМДПЩЃЛ
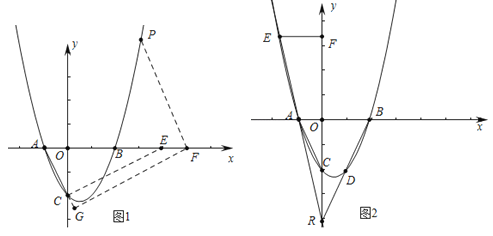
ЃЈ2ЃЉШчЭМ1жаЃЌзїCEЁЭACНЛxжсгкEЃЌдкxжсЩЯШЁвЛЕуFЃЌзїFGЁЭACгкGЃЌзїFPЁЮACЃЎЕБFG=![]() ЪБЃЌЕуPЕНжБЯпACЕФОрРывВЪЧ
ЪБЃЌЕуPЕНжБЯпACЕФОрРывВЪЧ![]() ЃЌДЫЪБвдPЮЊдВаФ
ЃЌДЫЪБвдPЮЊдВаФ![]() ЮЊАыОЖЕФдВЧЁКУгыACЯрЧаЃЌЯыАьЗЈЧѓГіжБЯпPFЕФНтЮіЪНЃЌРћгУЗНГЬзщЧѓНЛЕуPЕФжЕзјБъМДПЩЃЎ
ЮЊАыОЖЕФдВЧЁКУгыACЯрЧаЃЌЯыАьЗЈЧѓГіжБЯпPFЕФНтЮіЪНЃЌРћгУЗНГЬзщЧѓНЛЕуPЕФжЕзјБъМДПЩЃЎ
ЃЈ3ЃЉРћгУDR=DBЕУГіЕуDЕФзјБъЃЌЖјЕуDдкХзЮяЯпЩЯЃЌМДПЩЕУГіRЕФзјБъЃЌНјЖјЧѓГіжБЯпARЕФНтЮіЪНМДПЩЕУГіЕуEЕФзјБъЃЌЧѓГіEFЁЂABМДПЩНтОіЮЪЬтЃЎ
ЃЈ1ЃЉЁпХзЮяЯпy=aЃЈx2ЉcxЉ2c2ЃЉ=aЃЈx+cЃЉЃЈxЉ2cЃЉЃЌЁрAЃЈЉcЃЌ0ЃЉЃЌBЃЈ2cЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ2ac2ЃЉЃЌЕБAЃЈЉ1ЃЌ0ЃЉЪБЃЌЁрЉc=Љ1ЃЌЁрc=1ЃЌЁр2c=2ЃЌЁрBЃЈ2ЃЌ0ЃЉЃЎ
ЙЪД№АИЮЊЃКЃЈ2ЃЌ0ЃЉЃЎ
ЃЈ2ЃЉЁпa=1ЃЌc=1ЃЌЁрBЃЈ2ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ2ЃЉЃЌЁрХзЮяЯпЕФНтЮіЪНЮЊy=x2ЉxЉ2ЃЎ
ШчЭМ1жаЃЌзїCEЁЭACНЛxжсгкEЃЌдкxжсЩЯШЁвЛЕуFЃЌзїFGЁЭACгкGЃЌзїFPЁЮACЃЎ
ЕБFG=![]() ЪБЃЌЕуPЕНжБЯпACЕФОрРывВЪЧ
ЪБЃЌЕуPЕНжБЯпACЕФОрРывВЪЧ![]() ЃЌДЫЪБвдPЮЊдВаФ
ЃЌДЫЪБвдPЮЊдВаФ![]() ЮЊАыОЖЕФдВЧЁКУгыACЯрЧаЃЎ
ЮЊАыОЖЕФдВЧЁКУгыACЯрЧаЃЎ
ЁпЁЯOAC=ЁЯCAEЃЌЁЯAOC=ЁЯACE=90ЁуЃЌЁрЁїAOCЁзЁїACEЃЌЁр![]() =
=![]() =
=![]() =
=![]() =
=![]() ЃЌЁрAE=5ЃЌEC=
ЃЌЁрAE=5ЃЌEC=![]() ЃЎ
ЃЎ
ЁпECЁЮFGЃЌЁр![]() =
=![]() =
=![]() ЃЌЁрAF=6ЃЌЁрFЃЈ5ЃЌ0ЃЉЃЎ
ЃЌЁрAF=6ЃЌЁрFЃЈ5ЃЌ0ЃЉЃЎ
ЁпжБЯпACЕФНтЮіЪНЮЊy=Љ2xЉ2ЃЌЩшжБЯпPFЕФНтЮіЪНЮЊy=Љ2x+bЃЌАбЃЈ5ЃЌ0ЃЉДњШыЕУb=10ЃЌЁржБЯпPFЕФНтЮіЪНЮЊy=Љ2x+10ЃЌгЩ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁпЕуPдкЕквЛЯѓЯоЃЌЁрPЃЈ3ЃЌ4ЃЉЃЎ
ЃЈ3ЃЉШчЭМ2жаЃЌЁпDR=DBЃЌRЃЈ0ЃЌnЃЉЃЌBЃЈ2cЃЌ0ЃЉЃЌЁрDЃЈcЃЌ![]() nЃЉЃЎ
nЃЉЃЎ
ЁпЕуDдкХзЮяЯпy=aЃЈx2ЉcxЉ2c2ЃЉЩЯЃЌЁрaЃЈc2Љc2Љ2c2ЃЉ=![]() nЃЌЁрn=Љ4ac2ЃЌЁрRЃЈ0ЃЌЉ4ac2ЃЉЃЎ
nЃЌЁрn=Љ4ac2ЃЌЁрRЃЈ0ЃЌЉ4ac2ЃЉЃЎ
ЁпAЃЈЉcЃЌ0ЃЉЃЌЁржБЯпARЕФНтЮіЪНЮЊy=Љ4acxЉ4ac2ЂйЃЎ
ЁпЕуEдкХзЮяЯпy=aЃЈx+cЃЉЃЈxЉ2cЃЉЂкЩЯЃЌСЊСЂЂйЂкЕУЃКEЃЈЉ2cЃЌЉ12ac2ЃЉЃЌЁрEF=2cЃЌAB=3cЃЌЁр![]() =
=![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшжБЯпyЃНkx+6КЭжБЯпyЃНЃЈk+1ЃЉx+6ЃЈkЪЧе§ећЪ§ЃЉМАxжсЮЇГЩЕФШ§НЧаЮУцЛ§ЮЊSkЃЈkЃН1ЃЌ2ЃЌ3ЃЌЁЃЌ8ЃЉЃЌдђS1+S2+S3+Ё+S8ЕФжЕЪЧЃЈЁЁЁЁЃЉ
A. ![]() B.
B. ![]() C. 16D. 14
C. 16D. 14
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAЁЂBСНЕудкЪ§жсЩЯЃЌЕуAБэЪОЕФЪ§ЮЊЈC10ЃЌOB=4OAЃЌЕуMвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕуAПЊЪМЯђзѓдЫЖЏЃЌЕуNвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕуBПЊЪМЯђзѓдЫЖЏЃЈЕуMКЭЕуNЭЌЪБГіЗЂЃЉЃЎ

ЃЈ1ЃЉЪ§жсЩЯЕуBЖдгІЕФЪ§ЪЧ__________ЃЌЯпЖЮABЕФжаЕуCЖдгІЕФЪ§ЪЧ__________ЃЛ
ЃЈ2ЃЉОЙ§МИУыЃЌЕуMЁЂЕуNЕНдЕуЕФОрРыЯрЕШЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
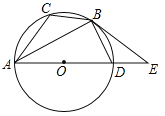
ЁОЬтФПЁПШчЭМЃЌвбжЊЁбOЪЧЁїABCЕФЭтНгдВЃЌADЪЧЁбOЕФжБОЖЃЌЧвBD=BCЃЌбгГЄADЕНEЃЌBEЪЧЁбOЕФЧаЯпЃЌBЪЧЧаЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯEBD=ЁЯCABЃЛ
ЃЈ2ЃЉШєBC=![]() ЃЌAC=5ЃЌЧѓsinЁЯCBAЃЎ
ЃЌAC=5ЃЌЧѓsinЁЯCBAЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТУцЮФзжЃЌШЛКѓЛиД№ЮЪЬтЃЎ
ДѓМвжЊЕР![]() ЪЧЮоРэЪ§ЃЌЖјЮоРэЪ§ЪЧЮоЯоВЛбЛЗаЁЪ§ЃЌЫљвд
ЪЧЮоРэЪ§ЃЌЖјЮоРэЪ§ЪЧЮоЯоВЛбЛЗаЁЪ§ЃЌЫљвд![]() ЕФаЁЪ§ВПЗжЮвУЧВЛПЩФмШЋВПаДГіРДЃЌгЩгк
ЕФаЁЪ§ВПЗжЮвУЧВЛПЩФмШЋВПаДГіРДЃЌгЩгк![]() ЕФећЪ§ВПЗжЪЧ1ЃЌНЋ
ЕФећЪ§ВПЗжЪЧ1ЃЌНЋ![]() МѕШЅЫќЕФећЪ§ВПЗжЃЌВюОЭЪЧЫќЕФаЁЪ§ВПЗжЃЌвђДЫ
МѕШЅЫќЕФећЪ§ВПЗжЃЌВюОЭЪЧЫќЕФаЁЪ§ВПЗжЃЌвђДЫ![]() ЕФаЁЪ§ВПЗжПЩгУ
ЕФаЁЪ§ВПЗжПЩгУ![]() Љ1БэЪОЃЎ
Љ1БэЪОЃЎ
гЩДЫЮвУЧЕУЕНвЛИіецУќЬтЃКШчЙћ![]() ЃНx+yЃЌЦфжаxЪЧећЪ§ЃЌЧв0ЃМyЃМ1ЃЌФЧУДxЃН1ЃЌyЃН
ЃНx+yЃЌЦфжаxЪЧећЪ§ЃЌЧв0ЃМyЃМ1ЃЌФЧУДxЃН1ЃЌyЃН![]() Љ1ЃЎ
Љ1ЃЎ
ЧыНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉШчЙћ![]() ЃНa+bЃЌЦфжаaЪЧећЪ§ЃЌЧв0ЃМbЃМ1ЃЌФЧУДaЃНЁЁ ЁЁЃЌbЃНЁЁ ЁЁЃЛ
ЃНa+bЃЌЦфжаaЪЧећЪ§ЃЌЧв0ЃМbЃМ1ЃЌФЧУДaЃНЁЁ ЁЁЃЌbЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉШчЙћЉ![]() ЃНc+dЃЌЦфжаcЪЧећЪ§ЃЌЧв0ЃМdЃМ1ЃЌФЧУДcЃНЁЁ ЁЁЃЌdЃНЁЁ ЁЁЃЛ
ЃНc+dЃЌЦфжаcЪЧећЪ§ЃЌЧв0ЃМdЃМ1ЃЌФЧУДcЃНЁЁ ЁЁЃЌdЃНЁЁ ЁЁЃЛ
ЃЈ3ЃЉвбжЊ2+![]() ЃНm+nЃЌЦфжаmЪЧећЕЃЌЧв0ЃМnЃМ1ЃЌЧѓ|mЉn|ЕФжЕЃЎ
ЃНm+nЃЌЦфжаmЪЧећЕЃЌЧв0ЃМnЃМ1ЃЌЧѓ|mЉn|ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕШБпЁїABCжаЃЌЕуDЃЌEЗжБ№дкБпBCЃЌABЩЯЃЌЧвBDЃНAEЃЌADгыCEНЛгкЕуFЃЌзїCMЁЭADЃЌДЙзуЮЊMЃЌЯТСаНсТлВЛе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ

A. ADЃНCE B. MFЃН![]() CF C. ЁЯBECЃНЁЯCDA D. AMЃНCM
CF C. ЁЯBECЃНЁЯCDA D. AMЃНCM
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуBЁЂEЁЂFЁЂCдквЛЬѕжБЯпЩЯЃЌAB=DE=10ЃЌAC=DFЃЌBE=CF=CEЃЎ
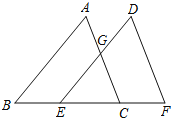
ЃЈ1ЃЉЧѓжЄЃКABЁЮDEЃЛ
ЃЈ2ЃЉЧѓEGЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
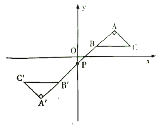
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЕФЖЅЕу
ЕФЖЅЕу![]() дкЕквЛЯѓЯоЃЌЕу
дкЕквЛЯѓЯоЃЌЕу![]() ЁЂ
ЁЂ![]() ЕФзјБъЗжБ№ЮЊ
ЕФзјБъЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌжБЯп
ЃЌжБЯп![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌШє
ЃЌШє![]() гы
гы![]() ЙигкЕу
ЙигкЕу![]() ГЩжааФЖдГЦЃЌдђЕу
ГЩжааФЖдГЦЃЌдђЕу![]() ЕФзјБъЮЊЃЈ ЃЉ
ЕФзјБъЮЊЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
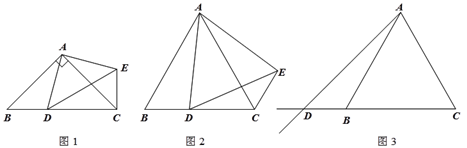
ЁОЬтФПЁПдкЁїABCжаЃЌAB=ACЃЌЕуDЪЧЩфЯпCBЩЯЕФвЛЖЏЕуЃЈВЛгыЕуBЁЂCжиКЯЃЉЃЌвдADЮЊвЛБпдкADЕФгвВрзїЁїADEЃЌЪЙAD=AEЃЌЁЯDAE=ЁЯBACЃЌСЌНгCEЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуDдкЯпЖЮCBЩЯЃЌЧвЁЯBAC=90ЁуЪБЃЌФЧУДЁЯDCE= ЖШЃЛ
ЃЈ2ЃЉЩшЁЯBAC= ![]() ЃЌЁЯDCE=
ЃЌЁЯDCE= ![]() ЃЎ
ЃЎ
Ђй ШчЭМ2ЃЌЕБЕуDдкЯпЖЮCBЩЯЃЌЁЯBACЁй90ЁуЪБЃЌЧыФуЬНОП![]() гы
гы![]() жЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
жЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
Ђк ШчЭМ3ЃЌЕБЕуDдкЯпЖЮCBЕФбгГЄЯпЩЯЃЌЁЯBACЁй90ЁуЪБЃЌЧыНЋЭМ3ВЙГфЭъећЃЌВЂжБНгаДГіДЫЪБ![]() гы
гы![]() жЎМфЕФЪ§СПЙиЯЕЃЈВЛашжЄУїЃЉЃЎ
жЎМфЕФЪ§СПЙиЯЕЃЈВЛашжЄУїЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com