
【题目】2015年4月25日14时11分,尼泊尔发生8.1级地震,震源深度20千米.中国救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧某面上选两探测点A、B,AB相距2米,探测线与该面的夹角分别是30°和45°(如图).试确定生命所在点C与探测面的距离.(参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=-![]() x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
(1)直接写出抛物线的解析式: ;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五边形ABCDE中,∠EAB=∠ABC=∠BCD=90°,AB=BC,且满足以点B为圆心,AB长为半径的圆弧AC与边DE相切于点F,连接BE,BD.
(1)如图1,求∠EBD的度数;
(2)如图2,连接AC,分别与BE,BD相交于点G,H,若AB=1,∠DBC=15°,求AGHC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数![]() 刻画,斜坡可以用一次函数y=
刻画,斜坡可以用一次函数y=![]() x刻画.
x刻画.
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在天水市汉字听写大赛中,10名学生得分情况如表
人数 | 3 | 4 | 2 | 1 |
分数 | 80 | 85 | 90 | 95 |
那么这10名学生所得分数的中位数和众数分别是( )
A.85和82.5
B.85.5和85
C.85和85
D.85.5和80
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知![]() (b、c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),点C的坐标为(4,3),直角顶点B在第四象限.
(b、c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),点C的坐标为(4,3),直角顶点B在第四象限.
(1)如图,若抛物线经过A、B两点,求抛物线的解析式.
(2)平移1中的抛物线,使顶点P在直线AC上并沿AC方向滑动距离为![]() 时,试证明:平移后的抛物线与直线AC交于x轴上的同一点.
时,试证明:平移后的抛物线与直线AC交于x轴上的同一点.
(3)在2的情况下,若沿AC方向任意滑动时,设抛物线与直线AC的另一交点为Q,取BC的中点N,试探究NP+BQ是否存在最小值?若存在,求出该最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有六张完全相同的卡片,其正面分别标有数字:﹣2,![]() ,π,0,
,π,0,![]() ,
,![]() ,将它们背面朝上洗匀后,从中随机抽取一张卡片,则其正面的数字为无理数的概率是 .
,将它们背面朝上洗匀后,从中随机抽取一张卡片,则其正面的数字为无理数的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,AB≠CD,BD=AC.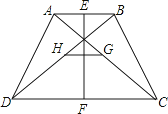
(1)求证:AD=BC
(2)若E、F、G、H分别是AB、CD、AC、BD的中点,求证:线段EF与线段GH互相垂直平分。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD内接于⊙O,∠ADC=90°,∠DCB<90°,对角线AC平分∠DCB,延长DA,CB相交于点E.
(1)如图1,EB=AD,求证:△ABE是等腰直角三角形;
(2)如图2,连接OE,过点E作直线EF,使得∠OEF=30°,当∠ACE≥30°时,判断直线EF与⊙O的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com