
【题目】如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数![]() 刻画,斜坡可以用一次函数y=
刻画,斜坡可以用一次函数y=![]() x刻画.
x刻画.
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标
【答案】
(1)
解:由题意得:![]() =
=![]() , 故二次函数图象的最高点P的坐标为(2,4);
, 故二次函数图象的最高点P的坐标为(2,4);
(2)
解:联立两解析式可得: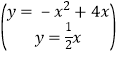 ,解得:
,解得:![]() ,或
,或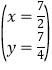 . 故可得点A的坐标为(
. 故可得点A的坐标为(![]() ,
,![]() );
);
(3)
解:如图,作PQ⊥x轴于点Q,AB⊥x轴于点B.

S△POA=S△POQ+S△梯形PQBA﹣S△BOA=![]() ×2×4+
×2×4+![]() ×(
×(![]() +4)×(
+4)×(![]() ﹣2)﹣
﹣2)﹣![]() ×
×![]() ×
×![]() =4+
=4+![]() ﹣
﹣![]() =
=![]() ;
;
(4)
解:过P作OA的平行线,交抛物线于点M,连结OM、AM,则△MOA的面积等于△POA的面积.

设直线PM的解析式为y=![]() x+b, ∵P的坐标为(2,4) ,∴4=
x+b, ∵P的坐标为(2,4) ,∴4=![]() ×2+b,解得b=3, ∴直线PM的解析式为y=
×2+b,解得b=3, ∴直线PM的解析式为y=![]() x+3.
x+3.
由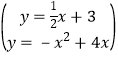 ,解得
,解得![]() ,或
,或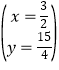 , ∴点M的坐标为(
, ∴点M的坐标为(![]() ,
,![]() ).
).
【解析】(1)利用配方法抛物线的一般式化为顶点式,即可求出二次函数图象的最高点P的坐标;(2)联立两解析式,可求出交点A的坐标;(3)作PQ⊥x轴于点Q,AB⊥x轴于点B.根据S△POA=S△POQ+S△梯形PQBA﹣S△BOA,代入数值计算即可求解;(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,由于两平行线之间的距离相等,根据同底等高的两个三角形面积相等,可得△MOA的面积等于△POA的面积. 设直线PM的解析式为y=![]() x+b,将P(2,4)代入,求出直线PM的解析式为y=
x+b,将P(2,4)代入,求出直线PM的解析式为y=![]() x+3.再与抛物线的解析式联立,得到方程组
x+3.再与抛物线的解析式联立,得到方程组 ,解方程组即可求出点M的坐标.
,解方程组即可求出点M的坐标.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】11月读书节,深圳市为统计某学校初三学生读书状况,如下图:
(1)求三本以上的x值、参加调查的总人数,并补全统计图;
(2)三本以上的圆心角为 ° .
(3)全市有6.7万学生,三本以上有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015广州)如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°
(1)利用尺规作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD(保留作图痕迹,不写作法)
(2)在(1)所作的图形中,求△ABE与△CDE的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图,△ABC是等腰三角形,AB=AC,请你用尺规作图将△ABC分成两个全等的三角形,并说明这两个三角形全等的理由.(保留作图痕迹,不写作法)
如图,△ABC是等腰三角形,AB=AC,请你用尺规作图将△ABC分成两个全等的三角形,并说明这两个三角形全等的理由.(保留作图痕迹,不写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年4月25日14时11分,尼泊尔发生8.1级地震,震源深度20千米.中国救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧某面上选两探测点A、B,AB相距2米,探测线与该面的夹角分别是30°和45°(如图).试确定生命所在点C与探测面的距离.(参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是边BC的中点,直线EF交正方形外角的平分线于点F,交DC于点G,且AE⊥EF.
(1)当AB=2时,求△GEC的面积;
(2)求证:AE=EF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清明期间,某校师生组成200个小组参加“保护环境,美化家园”植树活动.综合实际情况,校方要求每小组植树量为2至5棵,活动结束后,校方随机抽查了其中50个小组,根据他们的植树量绘制出如图所示的两幅不完整统计图.请根据图中提供的信息,解答下面的问题:
(1)请把条形统计图补充完整,并算出扇形统计图中,植树量为“5棵树”的圆心角是 ;
(2)请你帮学校估算此次活动共种多少棵树.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com