Question

【题目】（12分）如图，△ABC中，分别延长△ABC的边AB、AC到D、E，∠CBD与∠BCE的平分线相交于点P，爱动脑筋的小明在写作业的时发现如下规律：

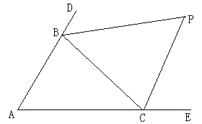
（1）若∠A＝50°，则∠P＝ °；

（2）若∠A＝90°，则∠P＝ °；

（3）若∠A＝100°，则∠P＝ °；

（4）请你用数学表达式归纳∠A与∠P的关系，并说明理由。

Answer 1

【答案】解：（1）∵∠A=50°，

∴∠ABC+∠ACB=180°-50°=130°，∠DBC+∠BCE=360°-130°=230°，

又∵∠CBD与∠BCE的平分线相交于点P，

∴∠PBC＝∠DBC，∠PCB＝∠ECB，

∴∠PBC+∠PCB＝（∠DBC+∠ECB）=115°，

∴∠P=65°．

同理得：（2）45°；

（3）40°

（4）∠P=90°-∠A．理由如下：

∵BP平分∠DBC，CP平分∠BCE，

∴∠DBC=2∠CBP，∠BCE=2∠BCP

又∵∠DBC=∠A+∠ACB∠BCE=∠A+∠ABC，

∴2∠CBP=∠A+∠ACB，2∠BCP=∠A+∠ABC，

∴2∠CBP+2∠BCP=∠A+∠ACB+∠A+∠ABC=180°+∠A，

∴∠CBP+∠BCP=90°+∠A

又∵∠CBP+∠BCP+∠P=180°，

∴∠P=90°-∠A．

【解析】试题分析：（1）若∠A=50°，则有∠ABC+∠ACB=130°，∠DBC+∠BCE=360°-130°=230°，根据角平分线的定义可以求得∠PBC+∠PCB的度数，再利用三角形的内角和定理即可求得∠P的度数；

（2）、（3）和（1）的解题步骤类似；（4）利用角平分线的性质和三角形的外角性质可求出∠BCP=（∠A+∠ABC），∠CBP=（∠A+∠ACB）；再利用三角形内角和定理即可求出∠A与∠P的关系．