
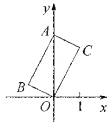
【题目】如图,在平面直角坐标系xOy中,四边形ABOC是矩形,点A在y轴上,若点C的坐标为(1,2),则点B的坐标为________.
【答案】(1,![]() )
)
【解析】
作CD⊥OA于D,BE⊥x轴于E,求出CD=1,OD=2,OC=![]() ,证明△AOC∽△COD,得
,证明△AOC∽△COD,得![]() ,求出OA=
,求出OA=![]() ,得出AD=OAOD=
,得出AD=OAOD=![]() ,证明△BOE≌△ACD(AAS),得出BE=AD=
,证明△BOE≌△ACD(AAS),得出BE=AD=![]() ,OE=CD=1,即可得出答案.
,OE=CD=1,即可得出答案.
解:作CD⊥OA于D,BE⊥x轴于E,如图所示:
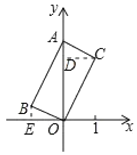
则∠CDA=∠OEB=90°,BE∥OA,
∴∠OBE=∠AOB,
∵点C的坐标为(1,2),
∴CD=1,OD=2,
∴OC=![]() ,
,
∵四边形ABOC是矩形,
∴OB=AC,AC∥OB,∠ACO=90°=∠CDA,
∴∠AOB=∠CAD,
∴∠OBE=∠CAD,
∵∠AOC=∠COD,
∴△AOC∽△COD,
∴![]() ,即
,即![]() ,
,
∴OA=![]() ,
,
∴AD=OAOD=![]() ,
,
在△BOE和△ACD中,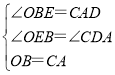 ,
,
∴△BOE≌△ACD(AAS),
∴BE=AD=![]() ,OE=CD=1,
,OE=CD=1,
∴点B的坐标为(1,![]() );
);
故答案为:(1,![]() ).
).


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:初中数学 来源: 题型:
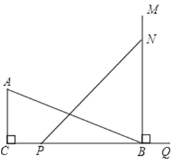
【题目】如图,CA⊥BC,垂足为C,AC=2Cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_______秒时,△BCA与点P、N、B为顶点的三角形全等.(2个全等三角形不重合)
查看答案和解析>>
科目:初中数学 来源: 题型:
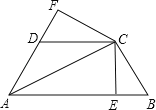
【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)若AB=15,AD=7,BC=5,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简再求值:
(1)![]() ,其中
,其中![]()
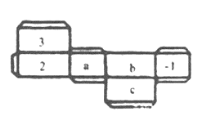
(2)如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
①填空:![]() _________,
_________,![]() _________
_________![]() _________;
_________;
②先化简,再求值:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
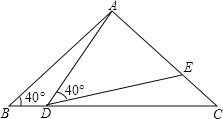
(1)若∠BDA=115°,则∠BAD= °,∠DEC= °;
(2)若DC=AB,求证:△ABD≌△DCE;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平行四边形ABCD,求作菱形AECF,使点E、点F分别在BC、AD边上
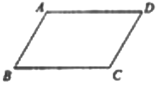
下面是小明设计的尺规作图过程.
作法:如图
① 连接AC;
② 分别以A、C为圆心,大于![]() AC的长为半径作弧,两弧交于M、N两点;
AC的长为半径作弧,两弧交于M、N两点;
③ 连接MN,分别与BC、AD、AC交于E、F、O三点;
④ 连接AE、CF
四边形AECF即为所求
根据小明设计的尺规作图过程
(1)使用直尺和圆规,补全图形:(保留作图痕迹)
(2)完成下面的证明
证明∵AM= ,AN= ,
∴MN是AC的垂直平分线。
( )(填推理的依据)
∴EF⊥AC,OA=OC,
∴平行四边形ABCD
∴AD∥BC
∴∠FAO=∠ECO
在△FAO和△ECO中

∴△FAO≌△ECO
∴OE=OF
又∵OA=OC
∴四边形AECF是平行四边形
( )(填推理依据)
∵EF⊥AC
∴四边形AECF是菱形
( )(填推理依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】日照间距系数反映了房屋日照情况.如图①,当前后房屋都朝向正南时,日照间距系数=L:(H﹣H1),其中L为楼间水平距离,H为南侧楼房高度,H1为北侧楼房底层窗台至地面高度.
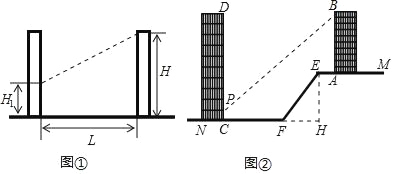
如图②,山坡EF朝北,EF长为15m,坡度为i=1:0.75,山坡顶部平地EM上有一高为22.5m的楼房AB,底部A到E点的距离为4m.
(1)求山坡EF的水平宽度FH;
(2)欲在AB楼正北侧山脚的平地FN上建一楼房CD,已知该楼底层窗台P处至地面C处的高度为0.9m,要使该楼的日照间距系数不低于1.25,底部C距F处至少多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1 (要求A与A1,B与B1,C与C1相对应);
(2)求△ABC的面积;
(3)在直线l上找一点P,使得△PAC的周长最小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某学校计划在教室内安装空气净化装置,需购进A、B两种设备,已知:购买1台A种设备和2台B种设备需要3.5万元;购买2台A种设备和1台B种设备需要2.5万元.
(1)求每台A种、B种设备各多少万元?
(2)根据学校实际,需购进A种和B种设备共30台,总费用不超过30万元,请你通过计算,求至少购买A种设备多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com