
【题目】已知△ABC的边AB是⊙O的弦.
(1)如图1,若AB是⊙O的直径,AB=AC,BC交⊙O于点D,且DM⊥AC于M,请判断直线DM与⊙O的位置关系,并给出证明;
(2)如图2,AC交⊙O于点E,若E恰好是![]() 的中点,点E到AB的距离是8,且AB长为24,求⊙O的半径长.
的中点,点E到AB的距离是8,且AB长为24,求⊙O的半径长.

【答案】(1)DM是⊙O的切线,证明见解析;(2)13.
【解析】(1)根据圆与等腰三角形的性质得出∠ODB=∠C,从而得到OD∥AC,再利用平行线的性质和切线的判定定理即可证明;
(2)利用垂径定理及勾股定理即可求解.
证明:(1)连接OD.
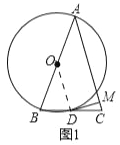
∵OB=OD,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∵DM⊥AC,
∴DM⊥OD,
∴DM是⊙O的切线.
(2)连接OA、连接OE交AB于点H,
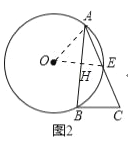
∵E 是![]() 中点,AB=24,
中点,AB=24,
∴OE⊥AB,AH=![]() AB=12,
AB=12,
连接OA,设OA=x,
∵EH=8,可得OH=x﹣8,
在Rt△OAH中,根据勾股定理可得(x﹣8)2+122=x2,
解得x=13,
∴⊙O的半径为13.


科目:初中数学 来源: 题型:
【题目】读一读:式子“1+2+3+4+5+……+100”表示从1开始的100个连续自然数的和.由于上述式子比较长,书写也不方便,为了简便起见,我们可将“1+2+3+4+5+……+100”表示为![]() ,这里“
,这里“![]() ”是求和符号.例如:“1+3+5+7+9+……+99”(即从1开始的100以内的连续奇数的和)可表示为
”是求和符号.例如:“1+3+5+7+9+……+99”(即从1开始的100以内的连续奇数的和)可表示为![]() ;又如“13+23+33+43+53+63+73+83+93+103”可表示为
;又如“13+23+33+43+53+63+73+83+93+103”可表示为![]() .同学们,通过对以上材料的阅读,请解答下列问题:
.同学们,通过对以上材料的阅读,请解答下列问题:
①2+4+6+8+10+……+100(即从2开始的100以内的连续偶数的和)用求和符号可表示为 ;
②计算:![]() = (填写最后的计算结果).
= (填写最后的计算结果).
③求:![]() 的值.(写出必要的过程)
的值.(写出必要的过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,当售价为每件60元时,每星期可卖出300件;现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.现在要使每星期利润为6125元,设每件商品应降价x元,则可列方程为( )
A. (20+x)(300+20x)=6125 B. (20-x)(300-20x)=6125
C. (20-x)(300+20x)=6125 D. (20+x)(300-20x)=6125
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察算式:![]() ;
;![]() ;
;![]() ;
;![]() ,...请根据你发现的规律填空:
,...请根据你发现的规律填空:
(1)![]() _________.
_________.
(2)用含n 的等式表示上面的规律:__________.
(3)用找到的规律解决下面的问题:计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣2ax﹣3a与y轴交于C点,交x轴于A、B,且OB=OC.
(1)求抛物线的解析式;
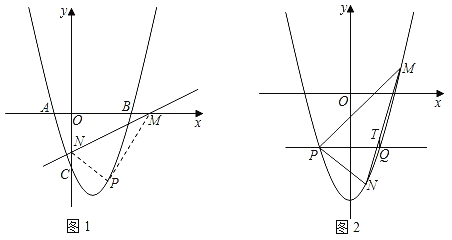
(2)如图1,直线l:y=![]() x+b(b<0)交x轴于M,交y轴于N.将△MON沿直线l翻折,得到△MPN,点O的对应点为P.若O的对应点P恰好落在抛物线上,求直线l的解析式;
x+b(b<0)交x轴于M,交y轴于N.将△MON沿直线l翻折,得到△MPN,点O的对应点为P.若O的对应点P恰好落在抛物线上,求直线l的解析式;
(3)如图2,将原抛物线向左平移1个单位,向下平移t个单位,得到新抛物线C1.若直线y=m与新抛物线C1交于P、Q两点,点M是新抛物线C1上一动点,连接PM,并将直线PM沿y=m翻折交新抛物线C1于N,过Q作QT∥y轴,交MN于点T,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
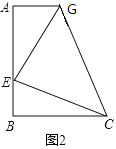
【题目】(1)如图,在正方形ABCD中,E是AB上一点,G是AD上一点,∠ECG=45°,那么EG与图中两条线段的和相等?证明你的结论.
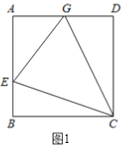
(2)请用(1)中所积累的经验和知识完成此题,如图,在四边形ABCG中,AG//BC(BC>AG),∠B=90°,AB=BC=12,E是AB上一点,且∠ECG=45°,BE=4,求EG的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x(千米) | 8 | 9 | 10 | 11.5 | 13 |
y1(分钟) | 18 | 20 | 22 | 25 | 28 |
(1)求y1关于x的函数表达式;
(2)李华骑单车的时间y2(单位:分钟)也受x的影响,其关系可以用y2=![]() x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师随手在黑板上写下了下列7个有理数:![]() ,0,
,0,![]() ,3,
,3,![]() ,-2019,-1.
,-2019,-1.
(1)请你指出哪些是整数?哪些是负整数?哪些是负分数?
(2)若选择其中的四个整数,将这四个整数经过有理数的混合运算后,能否得出结果为-1?若能,写出算式,并写出计算过程;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com