
【题目】图①、②分别是某种型号跑步机的实物图与示意图.已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到0.1m).
(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)
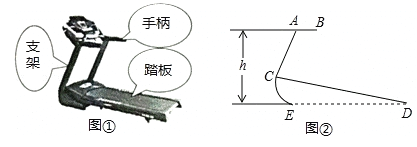
【答案】1.1m.
【解析】试题分析:过C点作FG⊥AB于F,交DE于G.在Rt△ACF中,根据CF=ACsin∠CAF求出CF的长,在Rt△CDG中,根据CG=CDsin∠CDE求出CG的长,然后根据FG=FC+CG计算即可.
试题解析:解:过C点作FG⊥AB于F,交DE于G.
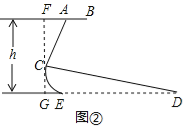
∵CD与地面DE的夹角∠CDE为12°,∠ACD为80°,
∴∠ACF=90°+12°﹣80°=22°,
∴∠CAF=68°,
在Rt△ACF中,CF=ACsin∠CAF≈0.744m,
在Rt△CDG中,CG=CDsin∠CDE≈0.336m,
∴FG=FC+CG≈1.1m.
故跑步机手柄的一端A的高度约为1.1m.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的个数为( ) ①柱体的上、下两个面一样大;②圆柱的侧面展开图是长方形;③正方体有6个顶点;④圆锥有2个面,且都是曲面;⑤球仅由1个面围成,这个面是平面;⑥三棱柱有5个面,且都是平面.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小彬和小明每天早晨坚持跑步,小彬每秒跑4米,小明每秒跑6米.
(1)如果他们站在百米跑道的两端同时相向起跑,那么几秒后两人相遇?
(2)如果小明站在百米跑道的起点处,小彬站在他前面10米处,两人同时同向起跑,几秒后小明能追上小彬?
(2)如果他们都站在四百米环形跑道的起点处,两人同时同向起跑,几分钟后他们再次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
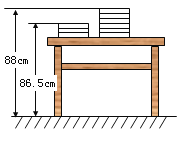
【题目】新学期,两摞规格相同的数学课本整齐的叠放在讲台上,请根据图中所给出的数据信息,解答下列问题:
(1)每本书的高度为 cm,课桌的高度为 cm;
(2)当课本数为x(本)时,请写出同样叠放在桌面上的一摞数学课本高出地面的距离 (用含x的代数式表示);
(3)桌面上有55本与题(1)中相同的数学课本,整齐叠放成一摞,若有18名同学各从中取走1本,求余下的数学课本高出地面的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
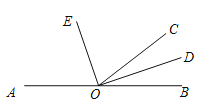
【题目】如图,已知点O是直线AB上的一点, ![]() ,OD、OE分别是
,OD、OE分别是![]() 、
、![]() 的角平分线.
的角平分线.
(1)求![]() 的度数;
的度数;
(2)写出图中与![]() 互余的角;
互余的角;
(3)图中有![]() 的补角吗?若有,请把它找出来,并说明理由.
的补角吗?若有,请把它找出来,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( ) 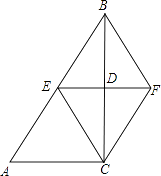
A.BC=AC
B.CF⊥BF
C.BD=DF
D.AC=BF
查看答案和解析>>
科目:初中数学 来源: 题型:
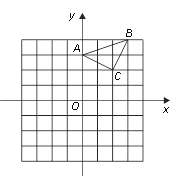
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中, 每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2︰1,并直接写出C2点的坐标及△A2BC2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题: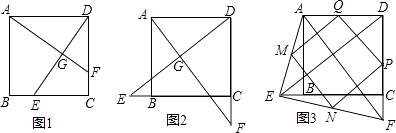
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com