
【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题: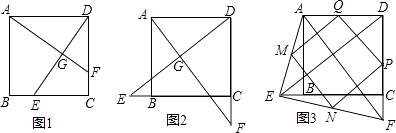
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
【答案】
(1)
解:上述结论①,②仍然成立,
理由为:∵四边形ABCD为正方形,
∴AD=DC,∠BCD=∠ADC=90°,
在△ADF和△DCE中,
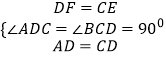 ,
,
∴△ADF≌△DCE(SAS),
∴AF=DE,∠DAF=∠CDE,
∵∠ADG+∠EDC=90°,
∴∠ADG+∠DAF=90°,
∴∠AGD=90°,即AF⊥DE
(2)
解:上述结论①,②仍然成立,
理由为:∵四边形ABCD为正方形,
∴AD=DC,∠BCD=∠ADC=90°,
在△ADF和△DCE中,
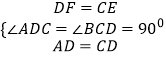 ,
,
∴△ADF≌△DCE(SAS),
∴AF=DE,∠CDE=∠DAF,
∵∠ADG+∠EDC=90°,
∴∠ADG+∠DAF=90°,
∴∠AGD=90°,即AF⊥D
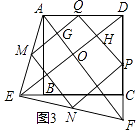
(3)
解:四边形MNPQ是正方形.
理由为:如图,设MQ,DE分别交AF于点G,O,PQ交DE于点H,
∵点M,N,P,Q分别为AE,EF,FD,AD的中点,
∴MQ=PN= ![]() DE,PQ=MN=
DE,PQ=MN= ![]() AF,MQ∥DE,PQ∥AF,
AF,MQ∥DE,PQ∥AF,
∴四边形OHQG是平行四边形,
∵AF=DE,
∴MQ=PQ=PN=MN,
∴四边形MNPQ是菱形,
∵AF⊥DE,
∴∠AOD=90°,
∴∠HQG=∠AOD=90°,
∴四边形MNPQ是正方形.
【解析】(1)由四边形ABCD为正方形,CE=DF,易证得△ADF≌△DCE(SAS),即可证得AF=DE,∠DAF=∠CDE,又由∠ADG+∠EDC=90°,即可证得AF⊥DE;(2)由四边形ABCD为正方形,CE=DF,易证得△ADF≌△DCE(SAS),即可证得AF=DE,∠E=∠F,又由∠ADG+∠EDC=90°,即可证得AF⊥DE;(3)首先设MQ,DE分别交AF于点G,O,PQ交DE于点H,由点M,N,P,Q分别为AE,EF,FD,AD的中点,即可得MQ=PN= ![]() DE,PQ=MN=
DE,PQ=MN= ![]() AF,MQ∥DE,PQ∥AF,然后由AF=DE,可证得四边形MNPQ是菱形,又由AF⊥DE即可证得四边形MNPQ是正方形.
AF,MQ∥DE,PQ∥AF,然后由AF=DE,可证得四边形MNPQ是菱形,又由AF⊥DE即可证得四边形MNPQ是正方形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
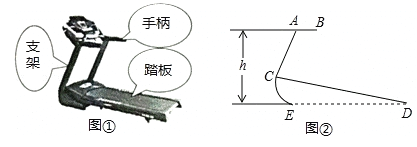
【题目】图①、②分别是某种型号跑步机的实物图与示意图.已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到0.1m).
(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式:![]() =1+
=1+ ![]() ﹣
﹣ ![]() =1
=1 ![]()
![]() =1+
=1+ ![]() ﹣
﹣ ![]() =1
=1 ![]()
![]() =1+
=1+ ![]() ﹣
﹣ ![]() =1
=1 ![]()
请你根据上面三个等式提供的信息,猜想:
(1)![]() =
=![]()
(2)请你按照上面每个等式反映的规律,写出用n(n为正整数)表示的等式:;
(3)利用上述规律计算: ![]() (仿照上式写出过程)
(仿照上式写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2的图象向右平移一个单位长度,再向下平移3个单位长度所得的图象解析式为( )
A.y=(x﹣1)2+3B.y=(x+1)2+3C.y=(x﹣1)2﹣3D.y=(x+1)2﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( ) 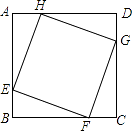
A.30
B.34
C.36
D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暴雨过后,某地遭遇山体滑坡,武警总队派出一队武警战士前往抢险. 半小时后,第二队前去支援,平均速度是第一队的1.5倍,结果两队同时到达.已知抢险队的出发地与灾区的距离为90千米,两队所行路线相同,问两队的平均速度分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com