
【题目】观察下列各式:![]() =1+
=1+ ![]() ﹣
﹣ ![]() =1
=1 ![]()
![]() =1+
=1+ ![]() ﹣
﹣ ![]() =1
=1 ![]()
![]() =1+
=1+ ![]() ﹣
﹣ ![]() =1
=1 ![]()
请你根据上面三个等式提供的信息,猜想:
(1)![]() =
=![]()
(2)请你按照上面每个等式反映的规律,写出用n(n为正整数)表示的等式:;
(3)利用上述规律计算: ![]() (仿照上式写出过程)
(仿照上式写出过程)
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数为( ) ①柱体的上、下两个面一样大;②圆柱的侧面展开图是长方形;③正方体有6个顶点;④圆锥有2个面,且都是曲面;⑤球仅由1个面围成,这个面是平面;⑥三棱柱有5个面,且都是平面.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( ) 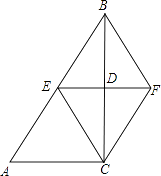
A.BC=AC
B.CF⊥BF
C.BD=DF
D.AC=BF
查看答案和解析>>
科目:初中数学 来源: 题型:
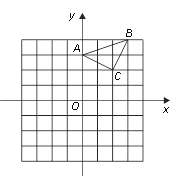
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中, 每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2︰1,并直接写出C2点的坐标及△A2BC2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判断四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.AB∥CD,AB=CD
C.AB=CD,AD∥BC
D.AB∥CD,AD∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
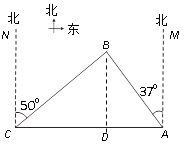
【题目】南中国海是中国固有领海,我渔政船经常在此海域执勤巡察.一天我渔政船停在小岛A北偏西37°方向的B处,观察A岛周边海域.据测算,渔政船距A岛的距离AB长为10海里.此时位于A岛正西方向C处的我渔船遭到某国军舰的袭扰,船长发现在其北偏东50°的方向上有我方渔政船,便发出紧急求救信号.渔政船接警后,立即沿BC航线以每小时30海里的速度前往救助,问渔政船大约需多少分钟能到达渔船所在的C处?
![]() (参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)
(参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题: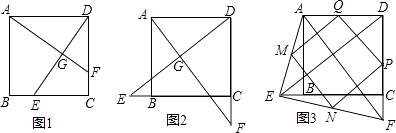
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B=__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com